Home
Class 12
MATHS
Two vertices of a triangle are (1, 3) an...

Two vertices of a triangle are (1, 3) and (4, 7). The orthocentre lies on the line `x + y = 3`. The locus of the third vertex is

A

`x^(2) - 2xy +2y^(2) - 3x - 4y +36 = 0`

B

`2x^(2)-4xy +3y^(2) - 4x - y +42 = 0`

C

`3x^(2)+xy - 4y^(2) - 2x +24y - 40 = 0`

D

`x^(2) - 4xy +3y^(2) - 2x - y +40 = 0`

Text Solution

Verified by Experts

The correct Answer is:
C

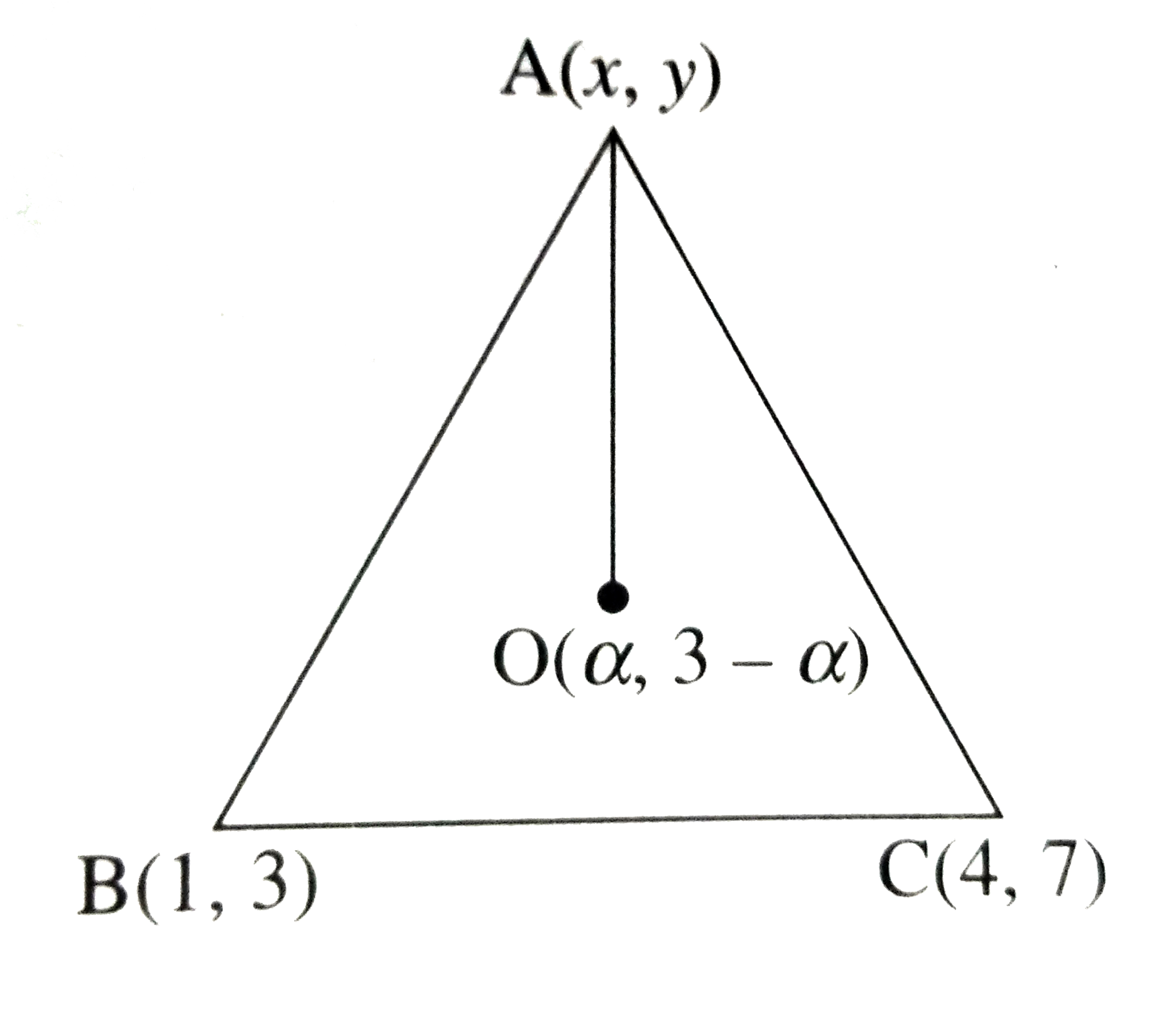
Orthocenter lies on the line `x +y = 2`
Let orthocenter be `O(alpha,3 -alpha)`
`BO _|_ AC`
`rArr (y-7)/(x-4) (alpha)/(1-alpha) =-1`
`rArr (alpha-1)/(alpha) =(y-7)/(x-4)`
`rArr 1-(1)/(alpha)=(y-7)/(x-4)`
`rArr (1)/(alpha)=1-(y-7)/(x-4)`
`rArr alpha =(x-4)/(x-y+3)`
Also, `AO _|_ BC`
`rArr (y-3+alpha)/(x-alpha) xx (4)/(3) =-1`
`rArr 4y =12 +4alpha =-3x +3 alpha`
`rArr alpha =-3x - 4y +12`
`:.` The locus is `(x-4)/(x-y+3) =- 3x -4y +12`
Promotional Banner

Topper's Solved these Questions

  • COORDINATE SYSTEM

    CENGAGE|Exercise Comprehension Type|4 Videos

  • COORDINATE SYSTEM

    CENGAGE|Exercise Multiple Correct Answers Type|2 Videos

  • CONTINUITY AND DIFFERENTIABILITY

    CENGAGE|Exercise Question Bank|22 Videos

  • COORDINATE SYSYEM

    CENGAGE|Exercise JEE Main Previous Year|6 Videos

Similar Questions

Explore conceptually related problems

Two vertices of a triangle are (5,-1) and (-2,3) .The orthocenter of the triangle is the origin. If the third vertex is (lambda,mu) then the value of 7 lambda-4 mu is

Two vertices of a triangle are (3,-1) and (-2,3) and its orthocentre is at the origin..Find the coordinates of eth third vertex.

Two vertices of a triangle are (5,-1) and (-2,3). If the orthocentre of the triangle is the origin,then the third vertex is

Two vertices of a triangle are A(2, 1) and B (3, -2) . The third vertex C lies on the line y=x+9 . If the centroid of DeltaABC lies on y-axis, find the coordinates of C and the centroid.

Two vertices of a triangle are (4,-3)&(-2,5). If the orthocentre of the triangle is at (1,2), find coordinates of the third vertex.

Two vertices of a triangle are (-2,-1) and (3,2) and third vertex lies on the line x+y=5. If the area of the triangle is 8 square units,then the third vertex is:

If two vertices of a triangle are (1,3) and (4,-1) e and the area of triangle is 5 sq.units,then the angle at the third vertex lies in: