A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- If the normal at a point P to the hyperbola meets the transverse axis ...
Text Solution
|
- If the normal at a pont P to the hyperbola x^2/a^2 - y^2/b^2 =1 meets ...
Text Solution
|
- Normal to a rectangular hyperbola at P meets the transverse axis at N....
Text Solution
|
- If asymptotes of hyperbola bisect the angles between the transverse ax...
Text Solution
|
- If the normal at a point P to the hyperbola meets the transverse axis ...
Text Solution
|
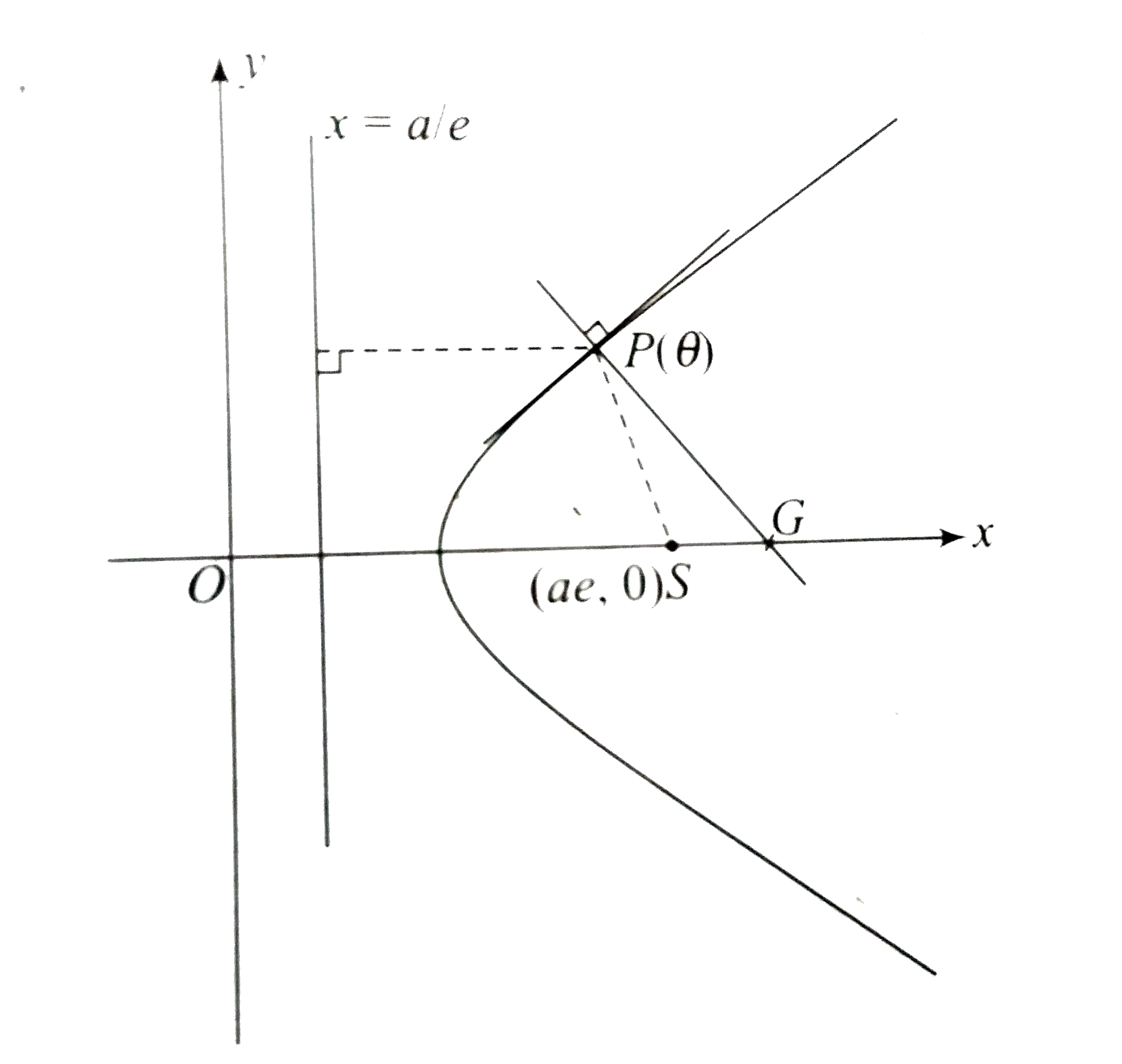
- Let 'S' be the focus and G be the point where the normal at P meets th...
Text Solution
|
- If the normal at the point P intersects the x-axis at (9, 0) then the ...
Text Solution
|
- If the normal at P on the hyperbola meets the transverse axis at G, S ...
Text Solution
|
- Let H be a hyperbola of eccentricity 3. A normal to the hyperbola meet...
Text Solution
|