Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN-APPLICATIONS OF DERIVATIVES-Exercise 6.5
- Find the maximum value of 2x^3-24 x+107in the interval [1, 3]. Find t...
Text Solution
|
- It is given that at x = 1, the function x^4-62 x^2+a x+9attains its m...
Text Solution
|
- Find the maximum and minimum values of x + sin2x on [0,2pi].
Text Solution
|
- Find two numbers whose sum is 24 and whose product is as large as p...
Text Solution
|
- Find two positive numbers x and y such that x + y = 60 and x y^3is ma...
Text Solution
|
- Find two positive numbers x and y such that their sum is 35 and the ...
Text Solution
|
- Find two positive numbers whose sum is 16 and the sum of whose cubes i...
Text Solution
|
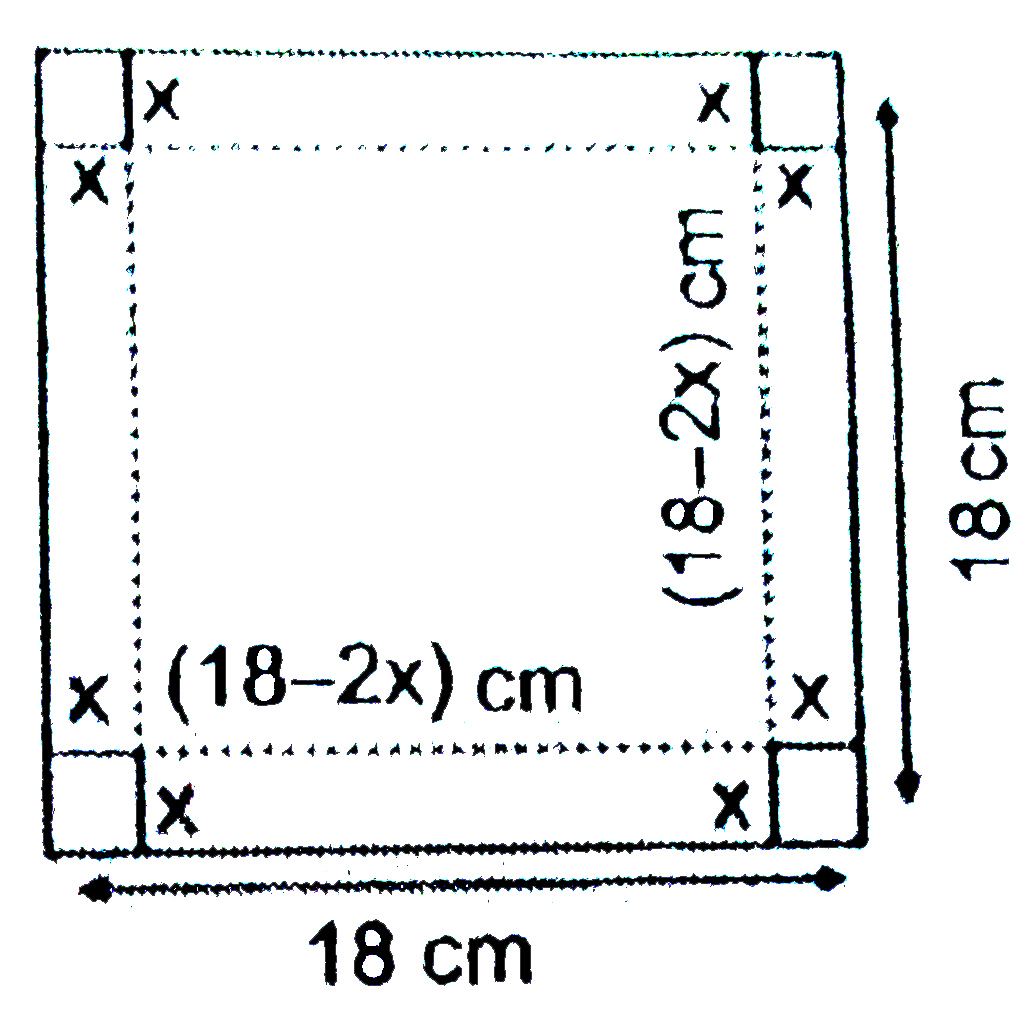
- A square piece of tin of side 18 cm is to be made into a box withou...
Text Solution
|
- A rectangular sheet of tin 45 cm by 24 cm is to be made into a box ...
Text Solution
|
- Show that of all the rectangles in a given fixed circle, the square h...
Text Solution
|
- Show that the right circular cylinder of given surface and maximum ...
Text Solution
|
- Of all the closed cylindrical cans (right circular), of a given volume...
Text Solution
|
- A wire of length 28 m is to be cut into two pieces. One of the piec...
Text Solution
|
- Prove that the volume of the largest cone, that can be inscribed in...
Text Solution
|
- Show that the right circular cone of least curved surface and given v...
Text Solution
|
- Show that the semi-vertical angle of the cone of the maximum volume a...
Text Solution
|
- Show that semi-vertical angle of right circular cone of given surface...
Text Solution
|
- The point on the curve x^2=2ywhich is nearest to the point (0, 5) is(A...
Text Solution
|
- For all real values of x, the minimum value of (1-x+x^2)/(1+x+x^2)is
Text Solution
|
- The maximum value of [x(x-1)+1]^(1/3), 0 le x le 1 is:
Text Solution
|