Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN-APPLICATIONS OF DERIVATIVES-Miscellaneous Exercise
- Show that the normal at any point theta to the curve x=acostheta+at...
Text Solution
|
- Find the intervals in which the function f given by f(x)=(4sinx-2x-x c...
Text Solution
|
- Find the intervals in which the function f given by f(x)=\ x^3+1/(...
Text Solution
|
- Find the maximum area of an isosceles triangle inscribed in the ellip...
Text Solution
|
- A tank with rectangular base and rectangular sides, open at the top is...
Text Solution
|
- The sum of the perimeter of a circle and square is k, where k is so...
Text Solution
|
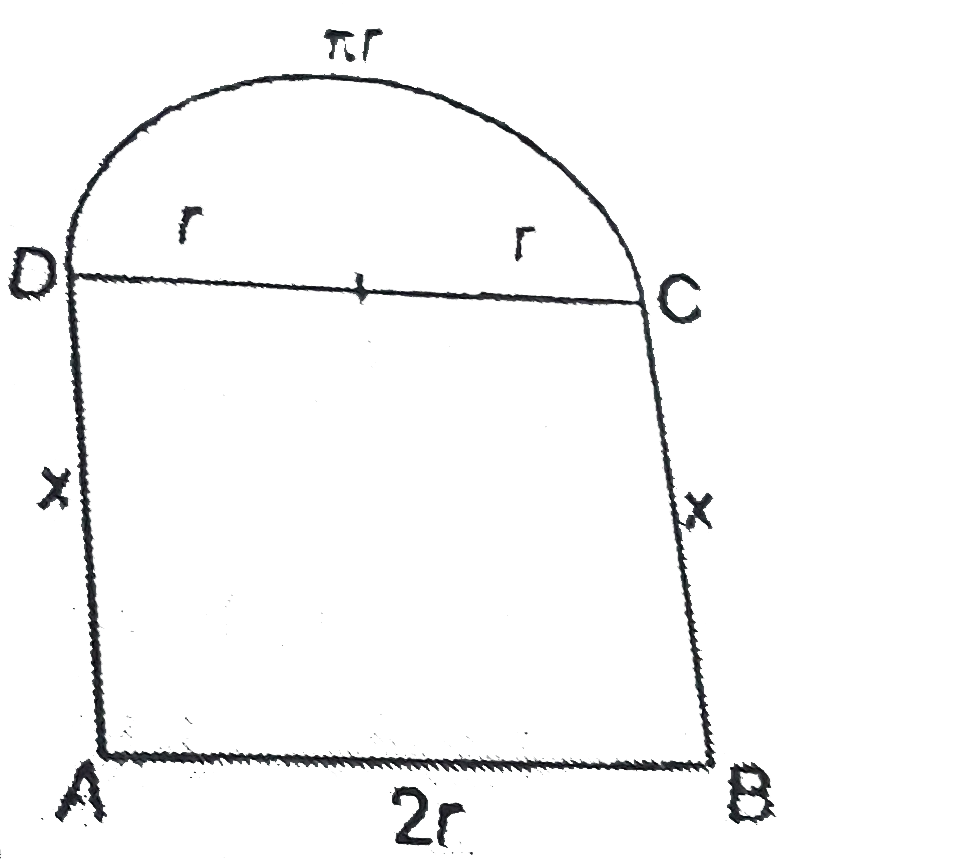
- A window is in the form of a rectangle surmounted by a semicircular...
Text Solution
|
- A point on the hypotenuse of a triangle is at distance a and b from t...
Text Solution
|
- Find the points at which the function f given by f(x)=(x-2)^4(x+1)^3 h...
Text Solution
|
- Find the absolute maximum and minimum values of the function f give...
Text Solution
|
- Show that the altitude of the right circular cone of maximum volume...
Text Solution
|
- Let f be a function defined on [a, b] such that f^(prime)(x)>0, for al...
Text Solution
|
- Show that the height of the cylinder of maximum volume that can be in...
Text Solution
|
- Show that height of the cylinder of greatest volume which can be insc...
Text Solution
|
- A cylindrical tank of radius 10 m is being filled with wheat at the r...
Text Solution
|
- The slope of the tangent to the curve x=t^2+3t-8,y=2t^2-2t-5at the po...
Text Solution
|
- The line y = m x + 1is a tangent to the curve y^2=4xif the value of m...
Text Solution
|
- The normal at the point (1,1) on the curve 2y+x^2=3 is
Text Solution
|
- The normal to the curve x^2=4y passing (1,2) is
Text Solution
|
- Find the point on the curve 9y^2=x^3, where the normal to the curve ma...
Text Solution
|