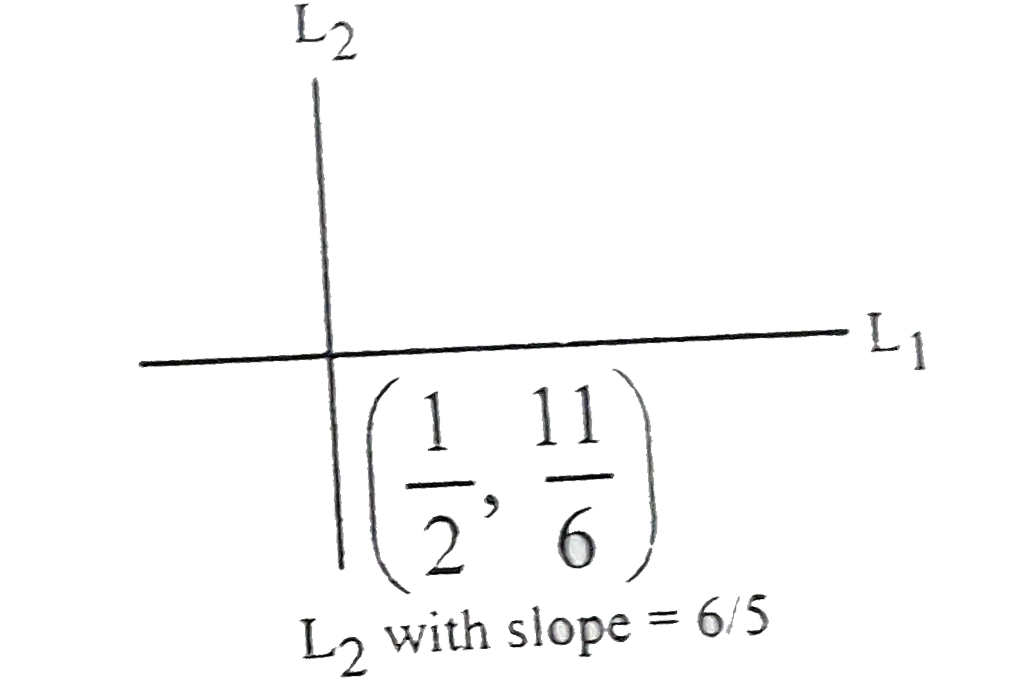Text Solution
Verified by Experts
Topper's Solved these Questions
TEST PAPERS
BANSAL|Exercise PHYSICS SECTION-1 Part-A (Single Correct choice Type )|5 VideosTEST PAPERS
BANSAL|Exercise PHYSICS SECTION-1 Part-A (Comprehension type )|3 VideosTEST PAPERS
BANSAL|Exercise Chemistry, SECTION-2 (PART-C)|10 VideosPROBABILITY
BANSAL|Exercise All Questions|1 VideosTHERMODYNAMICS
BANSAL|Exercise Match the column|7 Videos
Similar Questions
Explore conceptually related problems
BANSAL-TEST PAPERS-Mathematics, SECTION-3 (PART-C)
- If slope of one of the lines represented by 2x^(2)+2hxy+3y^(2)=0 is si...
Text Solution
|
- In triangle ABC," if " BC=8,angleB=30^(@),angleC=45^(@)" and "AD "is a...
Text Solution
|
- The line (a-1)x+ay=1 intersects the curve 3x^(2)+4xy+2y^(2)=1 at point...
Text Solution
|
- Find the number of solution of the equation (2sintheta-sin3theta)/(1+c...
Text Solution
|
- Let triangle ABC be an isosceles triangle with AB=AC. Suppose that the...
Text Solution
|
- Right triangle ABC with right angle A has an area equal to its perimet...
Text Solution
|
- If the equation of the circle throught the points of intersection of t...
Text Solution
|
- Suppose the line, L(1) has equation 10x-12y=-17." The line "L(2)"inter...
Text Solution
|
- A circle is inscribed in a right triangle ABC, right angled at C. The ...
Text Solution
|
- A variable line lx+my=1 (where l and m are parameters) intersect a cir...
Text Solution
|