Home
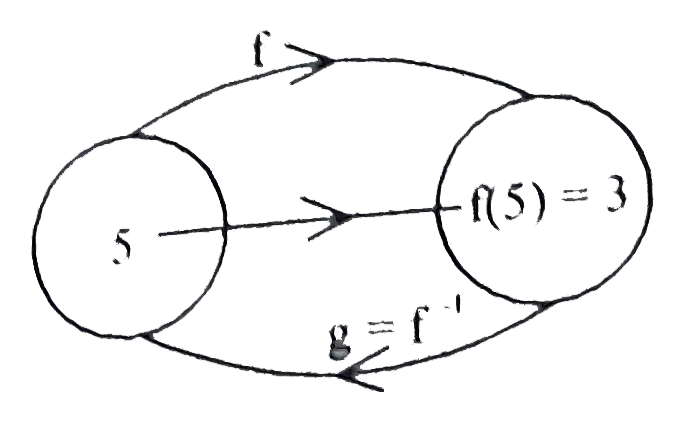
Class 12
MATHS
Suppose g is the inverse fiunction of a ...

Suppose g is the inverse fiunction of a diffdifferentiable finction fand `G(x)=(-4)/(g^2(x)).` If `f(5)=3 and f'(5)=1/125` then `g;(3)` is equal to

A

1

B

2

C

4

D

8

Text Solution

Verified by Experts

The correct Answer is:
A
`f(5)=3rArrg(3)=5`
`g'(y)=(1)/(f'(x))rArrg'(3)=(1)/(f'(5))=125`
`G'(x)=((-4)(-2))/(g^(3)(x)).g'(x)`
`G'(3)=(8)/(g^(3)(x))g'(x)=(8)/(125)xx125=8`.
Promotional Banner

Topper's Solved these Questions

  • TEST PAPERS

    BANSAL|Exercise MATHS SECTION - 2 PART A [PARAGRAPH TYPE]|6 Videos

  • TEST PAPERS

    BANSAL|Exercise MATHS SECTION - 2 [MULTIPLE CORRECT CHOICE TYPE]|6 Videos

  • TEST PAPERS

    BANSAL|Exercise CHEMISTRY SECTION - 2 [MULTIPLE CORRECT CHOICE TYPE]|6 Videos

  • PROBABILITY

    BANSAL|Exercise All Questions|1 Videos

  • THERMODYNAMICS

    BANSAL|Exercise Match the column|7 Videos

Similar Questions

Explore conceptually related problems

Suppose f^(-1) is the inverse function of a differentiable function f and let G(x)=(1)/(f^(-1)(x)) If f(3)=2 and f'(3)=(1)/(9), find G'(2)

Let g be the inverse function of a differentiable function f and G (x) =(1)/(g (x)). If f (4) =2 and f '(4) =(1)/(16), then the value of (G'(2))^(2) equals to:

Let g be the inverse function of f and f'(x)=(x^(10))/(1+x^(2)). If g(2)=a then g'(2) is equal to

Let g(x)=x^(3)-4x+6. If f'(x)=g(x) and f(1)=2, then what is f(x) equal to?

If g is the inverse function of f an f'(x)=(x^(5))/(1+x^(4)). If g(2)=a, then f'(2) is equal to

If g(x) is the inverse function of f(x) and f'(x)=(1)/(1+x^(4)) , then g'(x) is

If f(x) = 3x + 1 and g(x) = x^(2) - 1 , then (f + g) (x) is equal to

If g is the inverse of f and f'(x)=(1)/(2+x^(n)) then g'(x) is equal to