Home
Class 12
MATHS
A cloud chamber is a device, which makes...

A cloud chamber is a device, which makes the tracks of moving charged particles visible. A light charged particle collides with a nucleus and rebounds elastically. Which of the momentum vector diagrams shown below indicates the event to a good approximation.

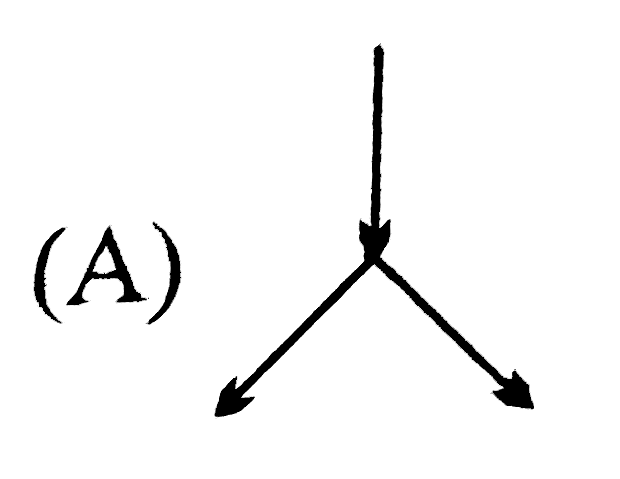
A

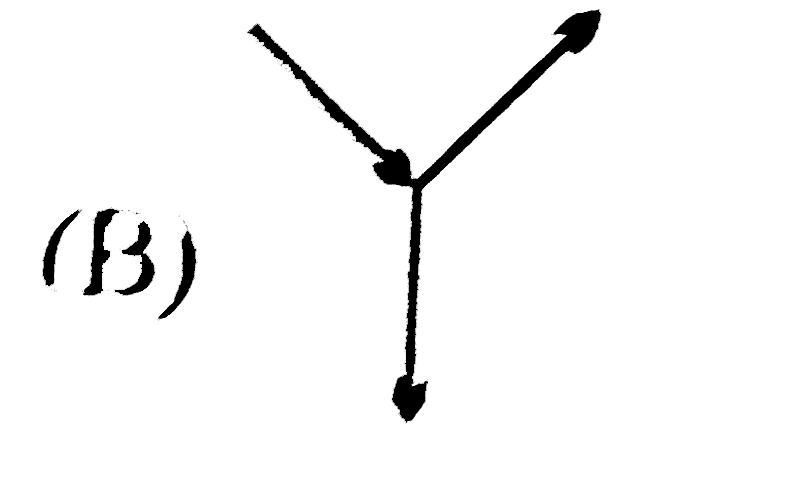
B

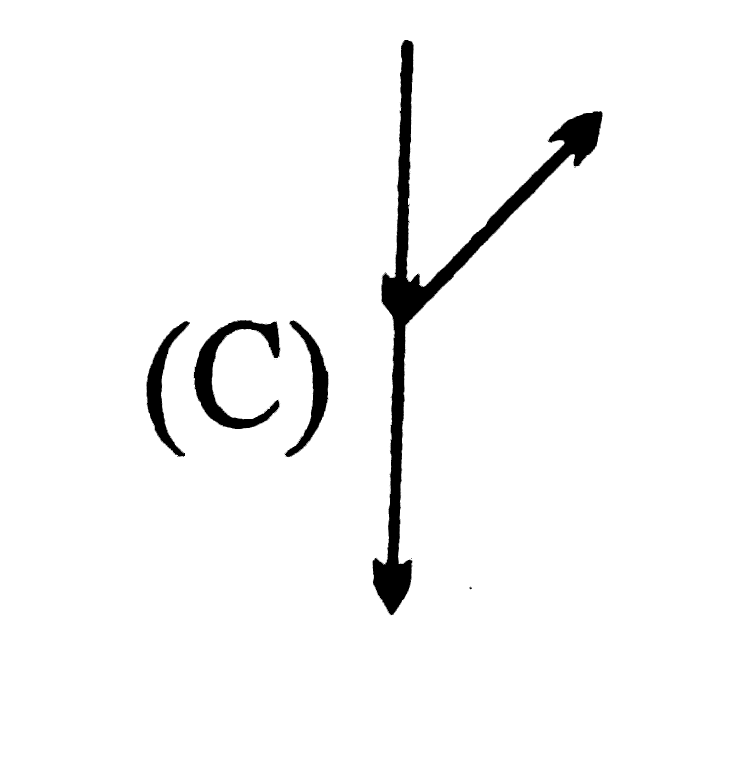
C

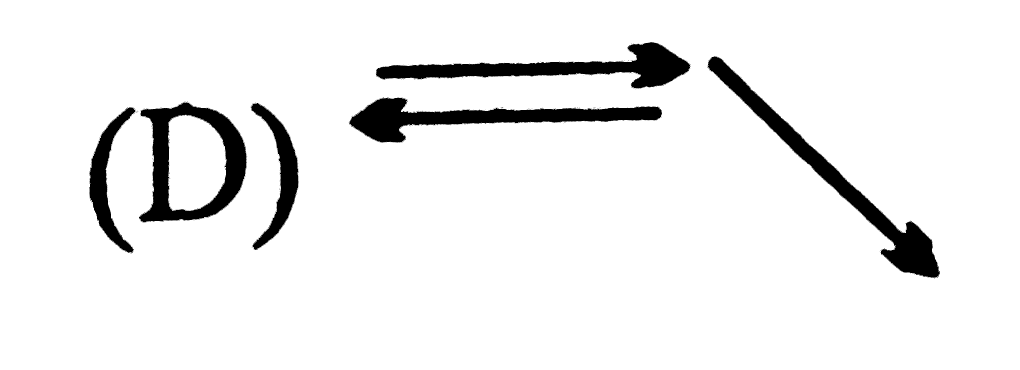
D

Text Solution

Verified by Experts

The correct Answer is:
B
Momentum is conserved only in option A and B, A is ruled out, because charged particle is lighter than the nucleus (and not of same mass)
Promotional Banner

Topper's Solved these Questions

  • TEST PAPERS

    BANSAL|Exercise CHEMISTRY|133 Videos

  • TEST PAPERS

    BANSAL|Exercise MATHEMATICS|58 Videos

  • TEST PAPERS

    BANSAL|Exercise MATHS SECTION - 2 [MULTIPLE CORRECT CHOICE TYPE]|6 Videos

  • PROBABILITY

    BANSAL|Exercise All Questions|1 Videos

  • THERMODYNAMICS

    BANSAL|Exercise Match the column|7 Videos

Similar Questions

Explore conceptually related problems

A charge particle moves along the line AB, which lies in the same plane of a circular loop of conduting wire as shown in the fig . Then :

A figure below shows the forces that three charged particles exert on each other. Which of the four situations shown can be correct .

Rutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's alpha -scattering experiment. If an alpha -particle is projected from infinity with speed v towards the nucleus having Z protons, then the alpha -particle which is reflected back or which is deflected by 180^@ must have approached closest to the nucleus .It can be approximated that alpha particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then: (P.E.)_i= 0 , since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back. 1/2m_alpha v_alpha^2+0=0+(Kq_1q_2)/Rimplies 1/2m_alphav_alpha^2=K(2exxZe)/R implies R=(4KZe^2)/(m_alphav_alpha^2) Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it An alpha -particle with initial speed v_0 is projected from infinity and it approaches up to r_0 distance from a nuclie. Then, the initial speed of alpha -particle, which approaches upto 2r_0 distance from the nucleus is :

Read the following passage carefully and answer the questions The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's alpha- scattering experiment. If an alpha- perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha- perticle which is reflected back or which is deflected by 180^(@) must have approach closest to the nucleus. It can be approximated that alpha- particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then: ("Total Energy")_("initial") = ("Total Enregy")_("final") (KE)_(i) +(PE)_(i)=(KE)_(f)+(PE)_(f) (PE)_(i) =0, "since"PE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back. 1/2m_(alpha)v_(alpha)^(2) + 0=0 + (kq_(1)q_(2))/(R) rArr1/2m_(alpha)v_(alpha)^(2)=k(2exxze)/(R)rArrR=(4kze^(2))/(m_(alpha)v_(alpha)^(2) Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as R=R_(0)(A)^(1//3) where R_(0) = 1.2xx10^(-15)m A= atomic mass number R=radius of nucleus If alpha- particle with speed v_(0) is projected from infinity and it approaches upto r_(0) distance from the nuclei. Then the speed of alpha- particle which approaches 2r_(0) distance from the nucleus is

Read the following passage carefully and answer the questions The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's alpha- scattering experiment. If an alpha- perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha- perticle which is reflected back or which is deflected by 180^(@) must have approach closest to the nucleus. It can be approximated that alpha- particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then: ("Total Energy")_("initial") = ("Total Enregy")_("final") (KE)_(i) +(PE)_(i)=(KE)_(f)+(PE)_(f) (PE)_(i) =0, "since"PE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back. 1/2m_(alpha)v_(alpha)^(2) + 0=0 + (kq_(1)q_(2))/(R) rArr1/2m_(alpha)v_(alpha)^(2)=k(2exxze)/(R)rArrR=(4kze^(2))/(m_(alpha)v_(alpha)^(2) Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as R=R_(0)(A)^(1//3) where R_(0) = 1.2xx10^(-15)m A= atomic mass number R=radius of nucleus Radius of a particular nucleus is calculated by the projection of alpha- particle from infinity at a particular speed. Let this radius be the true radius. If the radius calculation for the same nucleus is made by , alpha- particle with half of the earlier speed then the percentage error involved in the radius calculation is :

Read the following passage carefully and answer the questions The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's alpha- scattering experiment. If an alpha- perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha- perticle which is reflected back or which is deflected by 180^(@) must have approach closest to the nucleus. It can be approximated that alpha- particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then: ("Total Energy")_("initial") = ("Total Enregy")_("final") (KE)_(i) +(PE)_(i)=(KE)_(f)+(PE)_(f) (PE)_(i) =0, "since"PE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back. 1/2m_(alpha)v_(alpha)^(2) + 0=0 + (kq_(1)q_(2))/(R) rArr1/2m_(alpha)v_(alpha)^(2)=k(2exxze)/(R)rArrR=(4kze^(2))/(m_(alpha)v_(alpha)^(2) Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as R=R_(0)(A)^(1//3) where R_(0) = 1.2xx10^(-15)m A= atomic mass number R=radius of nucleus If the diameter of two different nuclei are in the ratio 1:2 then their mass number are in the ratio:

A particle with positive charge Q is held fixed at the origen. A second particle with positive charge q is fired at the first paricle, which follows the trajectory as shown in fig. (a) Is the angular momentum of the second particular momentum of the second particle constant about some axis? Why or why not? Give reason to support your answer. (b) Does the Coulomb force that one charge exerts on other charges changes if the other charges are brought nearby?(yes/No)

BANSAL-TEST PAPERS-PHYSICS
  1. A Bohr hydrogen atom undergoes a transition n=5rarrn=4 and emits a pho...

    Text Solution

    |

  2. A stream of photons with energy 4.4eV strike a metal surface with work...

    Text Solution

    |

  3. When the voltage applied to an X-ray tube increased from V(1)15.5 KV...

    Text Solution

    |

  4. When a certain metallic surface is irradiated with monochromatic lig...

    Text Solution

    |

  5. Figure shows the graph of photocurrent versus potential of the anod...

    Text Solution

    |

  6. The energy level diagram of a hypothetical atom is shown in the figu...

    Text Solution

    |

  7. Suppose frequency of emitted photon is of when electron of a stationar...

    Text Solution

    |

  8. A cloud chamber is a device, which makes the tracks of moving charged ...

    Text Solution

    |

  9. The nuclear binding energies of the elements P and Q are E(P) and E(Q...

    Text Solution

    |

  10. A radioactive substance with decay constant of 0.5s^(-1) is being prod...

    Text Solution

    |

  11. Rydberg atoms are nearly classical atoms in which electron is excited ...

    Text Solution

    |

  12. Rydberg atoms are nearly classical atoms in which electron is excited ...

    Text Solution

    |

  13. The first nuclear reaction ever observed was by ernest Rutherford in 1...

    Text Solution

    |

  14. The first nuclear reaction ever observed was by ernest Rutherford in 1...

    Text Solution

    |

  15. In an electron transition inside a hydrogen atom, orbital angular mome...

    Text Solution

    |

  16. Which of the following are not dependent on the intensity of the inci...

    Text Solution

    |

  17. Consider a beam of light of power 7.2 W incident on a prism of angle ...

    Text Solution

    |

  18. An electron orbiting around the nucleus of an atom

    Text Solution

    |

  19. Shows the energy-level diagram of hydrogen like imaginary element X. (...

    Text Solution

    |

  20. The .^(238)U nucleus has a binding energy of about 7.6 MeV per nucleon...

    Text Solution

    |