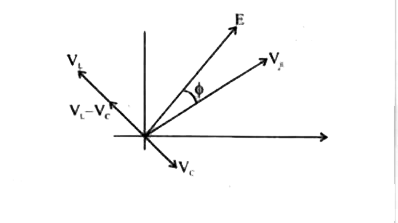
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NEW JOYTHI PUBLICATION-ALTERNATING CURRENT -OBJECTIVE TYPE QUESTION
- An LCR circuit consists of L = 230 mH, C = 70 mu F and R = 200 Omega ...
Text Solution
|
- In an LCR series circuit, at resonance
Text Solution
|
- A step down transformer increases the input current 4 A to 24 A at the...
Text Solution
|
- Transformer is used to
Text Solution
|
- If an LCR series circuit is connected to an ac source, then at resonan...
Text Solution
|
- A dynamo converts
Text Solution
|
- A transformer connected to 220 V mains is used to light a lamp of rati...
Text Solution
|
- A lamp consumes only 25% of the peak power in an ac circuit. The phase...
Text Solution
|