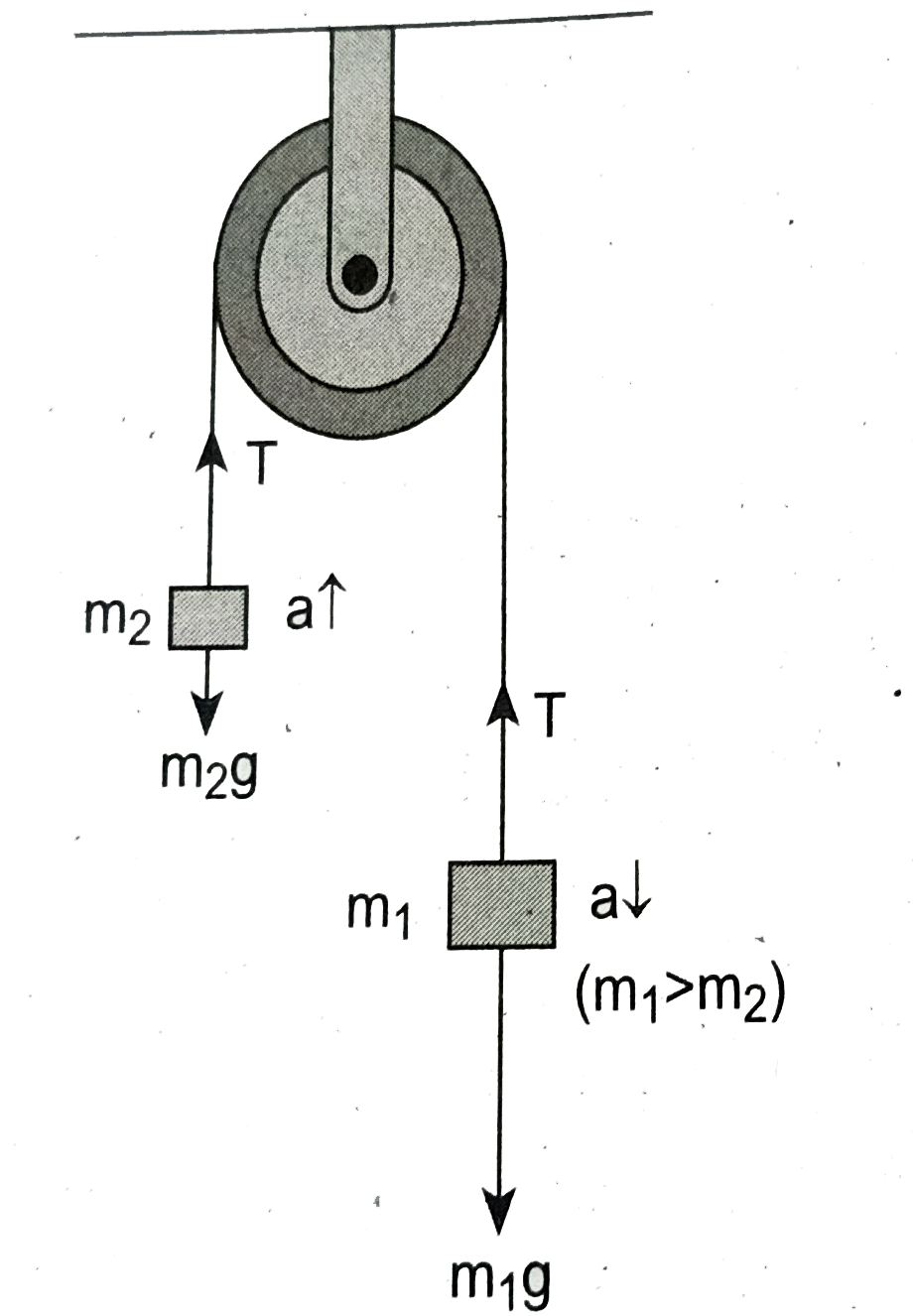
Vertical motion: Consider two blocks of masses `m_(1)` and `m_(2) (m_(2) gt m_(1))` connected by a light and inextensible string that passes over a pulley as shown in Figure. Let the tension in the string be T and acceleration a. When the system is released, both the blocks start moving,`m_(2)` vertically upward and `m_(1)` downward with same acceleration a. The gravitational force `m_(1)g` on mass `m_(1)` is used in lifting the mass `m_(2)`
The upward direction is chosen as y direction. The free body diagrams of both masses are shown in Figure.
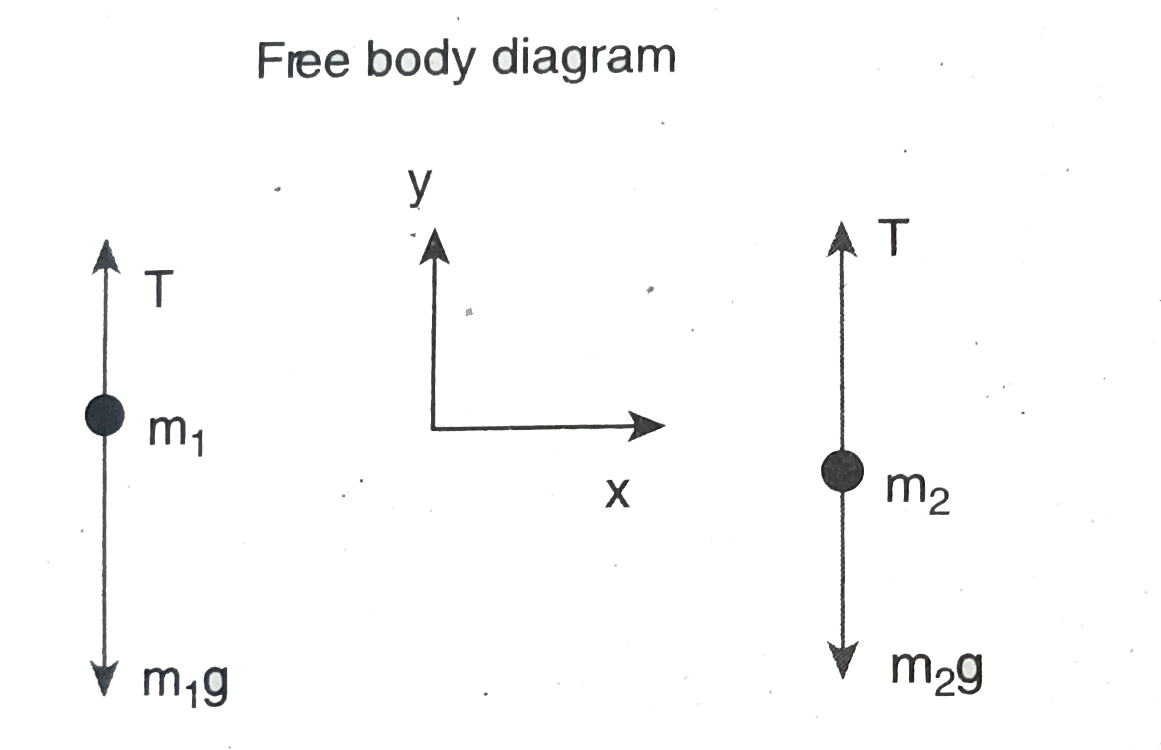
Applying Newton.s second law for mass `m_(2)`
`T hat j- m_(2)g hat j= m_(2)a hat j`
The left hand side of the above equation is the total force that acts on `m_(2)` and the right hand side is the product of mass and acceleration of `m_(2)` in y direction. By comparing the components on both sides, we get
`T- m_(2)g= m_(2)a`
Similarly, applying Newton.s second law for mass `m_(1)`
`T hat j- m_(1)g hat j= -m_(1)a hat j`
As mass `m_(1)` moves downward (`-hat j`), its acceleration is along (`-hat j`)
By comparing the components on both sides, we get
`T- m_(1)g= -m_(1)a`
`m_(1)g-T= m_(1)a`
Adding equations (1) and (2), we get
`m_(1)g-m_(2)g = m_(1)a+ m_(2)a`
`(m_(1)-m_(2))g= (m_(1)+m_(2))a`
From equation (3), the acceleration of both the masses is
`a= ((m_(1)-m_(2))/(m_(1)+m_(2)))g`
If both the masses are equal (`m_(1) = m_(2)`), from equation (4)
a=0
This shows that if the masses are equal, there is no acceleration and the system as a whole will be at rest. To find the tension acting on the string, substitute the acceleration from the equation (4) into the equation (1).
`T-m_(2)g= m_(2)((m_(1)-m_(2))/(m_(1)+m_(2)))g`
`T= m_(2)g+ m_(2)((m_(1)-m_(2))/(m_(1)+m_(2)))g`
By taking m,g common in the RHS of equation (5)
`T= m_(2)g(1+ (m_(1)-m_(2))/(m_(1)+m_(2)))`
`T= m_(2)g((m_(1)+m_(2)+ m_(1)-m_(2))/(m_(1)+m_(2)))`
`T= (2m_(1)m_(2))/(m_(1)+m_(2))g`
Equation (4) gives only magnitude of acceleration.
For mass `m_(1)` the acceleration vector is given by `vec a= -((m_(1)-m_(2))/(m_(1)+m_(2)))g hatj`
For mass m, the acceleration vector is given by `vec a= -((m_(1)-m_(2))/(m_(1)+m_(2)))g hatj`

