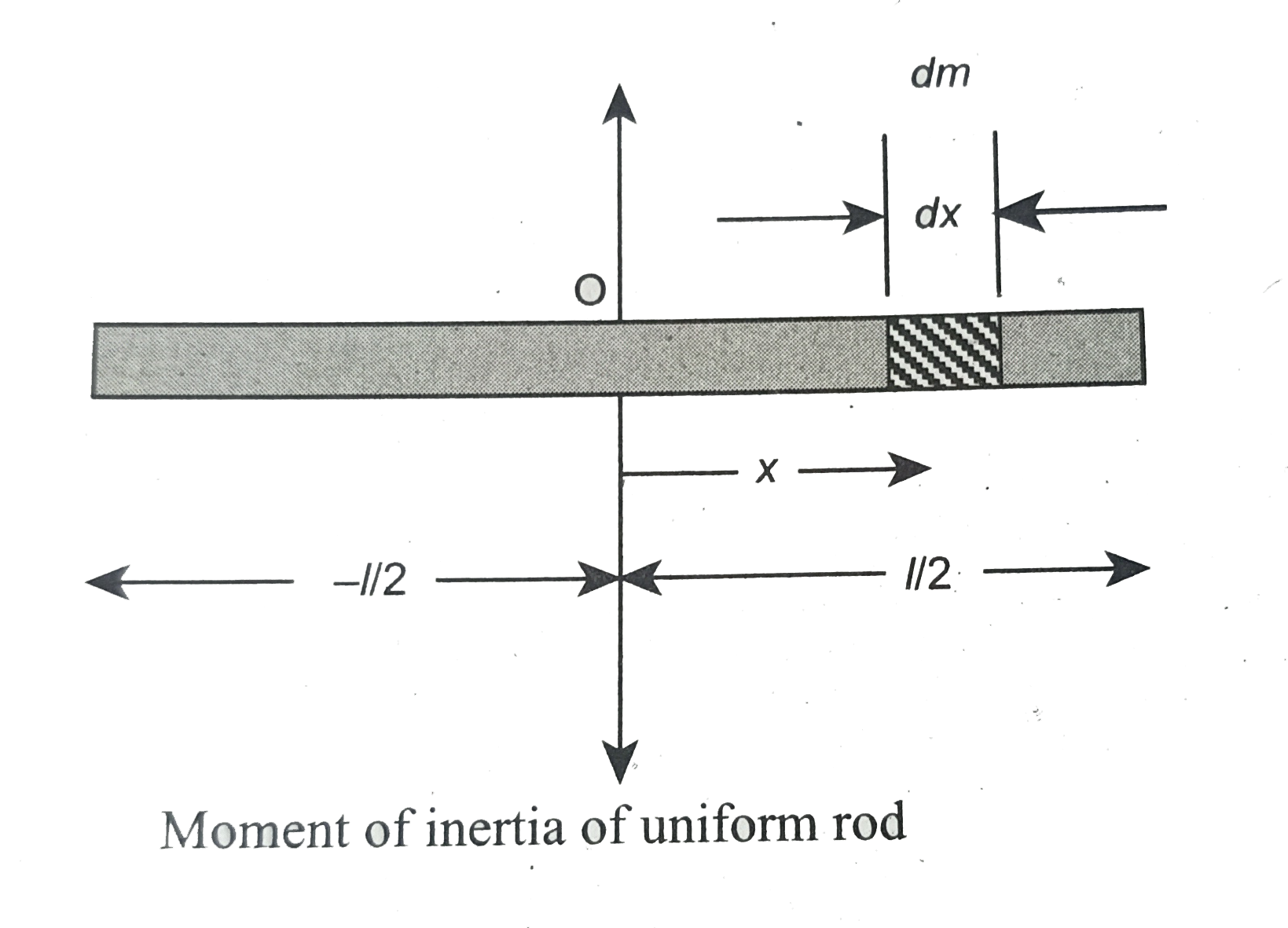
Text Solution
Verified by Experts
FULL MARKS-EXAMINATION QUESTION PAPER - JUNE 2019-PART IV
- Explain in detail the triangle law of addition.
Text Solution
|
- Explain in detail the four different types of oscillations.
Text Solution
|
- Explain the motion of blocks connected by a string in (i) vertical mot...
Text Solution
|
- What are stationary waves? write down the characteristics of stationar...
Text Solution
|
- Derive the expression for moment of inerita of a uniform disc about an...
Text Solution
|
- Ideal gas equation for n mole of gas
Text Solution
|
- Derive an expression for escape speed.
Text Solution
|
- Explain the different types of modulus of elasticity.
Text Solution
|
- Two objects of masses 2 kg and 4 kg are moving with the same momentum ...
Text Solution
|
- In a series of successive measurements in an experiment, the readings ...
Text Solution
|