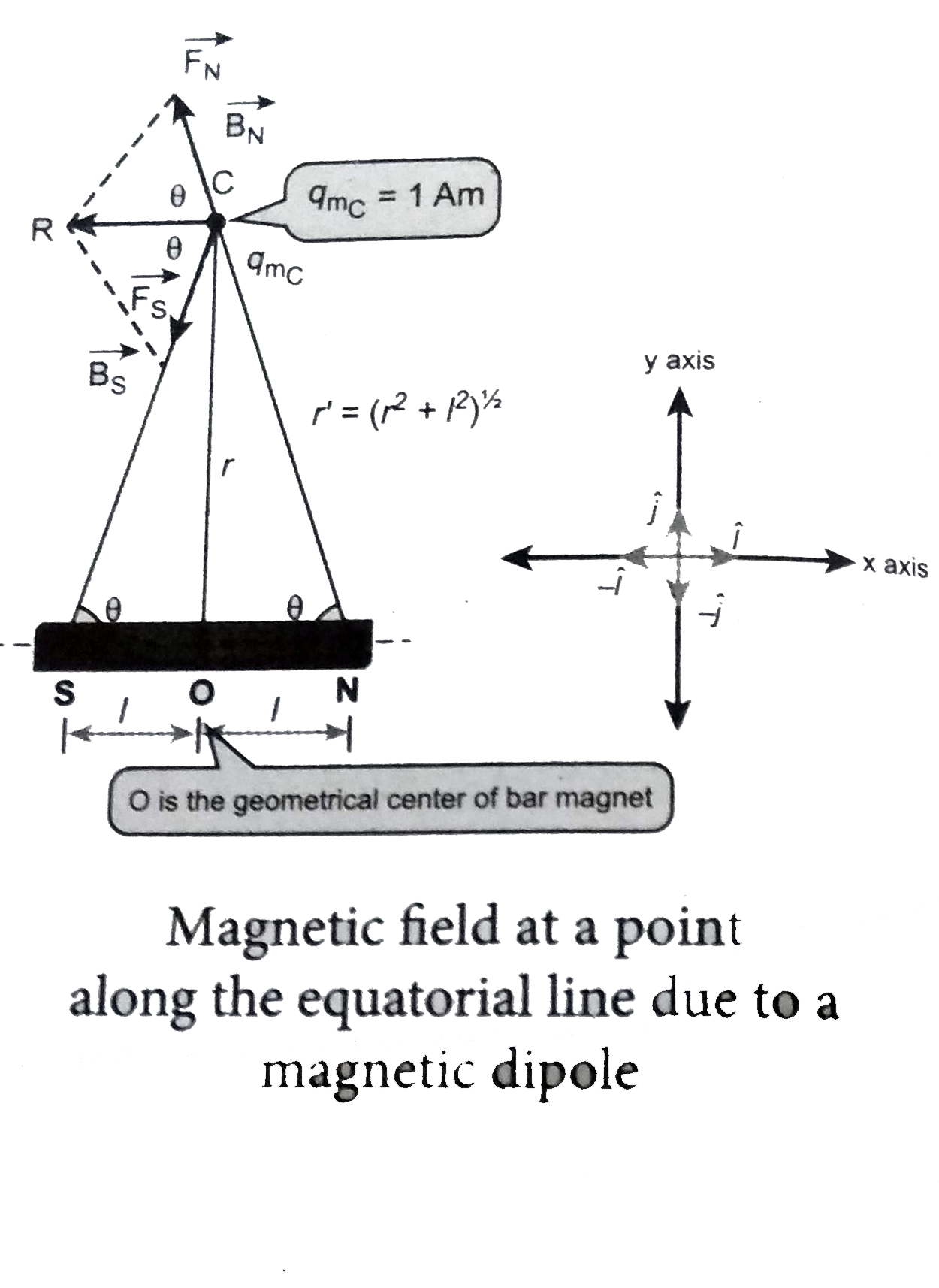
Magnetic field at a point along the equatorial line due to a magnetic dipole (bar magnet) Consider a bar magnet NS. Let N be the north pole and be the south pole of the bar magnet, each with pole strength `q_(m)`and separated by a distance of 2l. The magnetic field (lies along the equatorial line) at a distance r from the geometrical center of the bar mao can be computed by keeping unit north pole`(q_(m)C=1Am)` at C. The force experience the unit north pole at C due to pole strength N-S can be computed using Coulomb.s law of magnetism as follows:
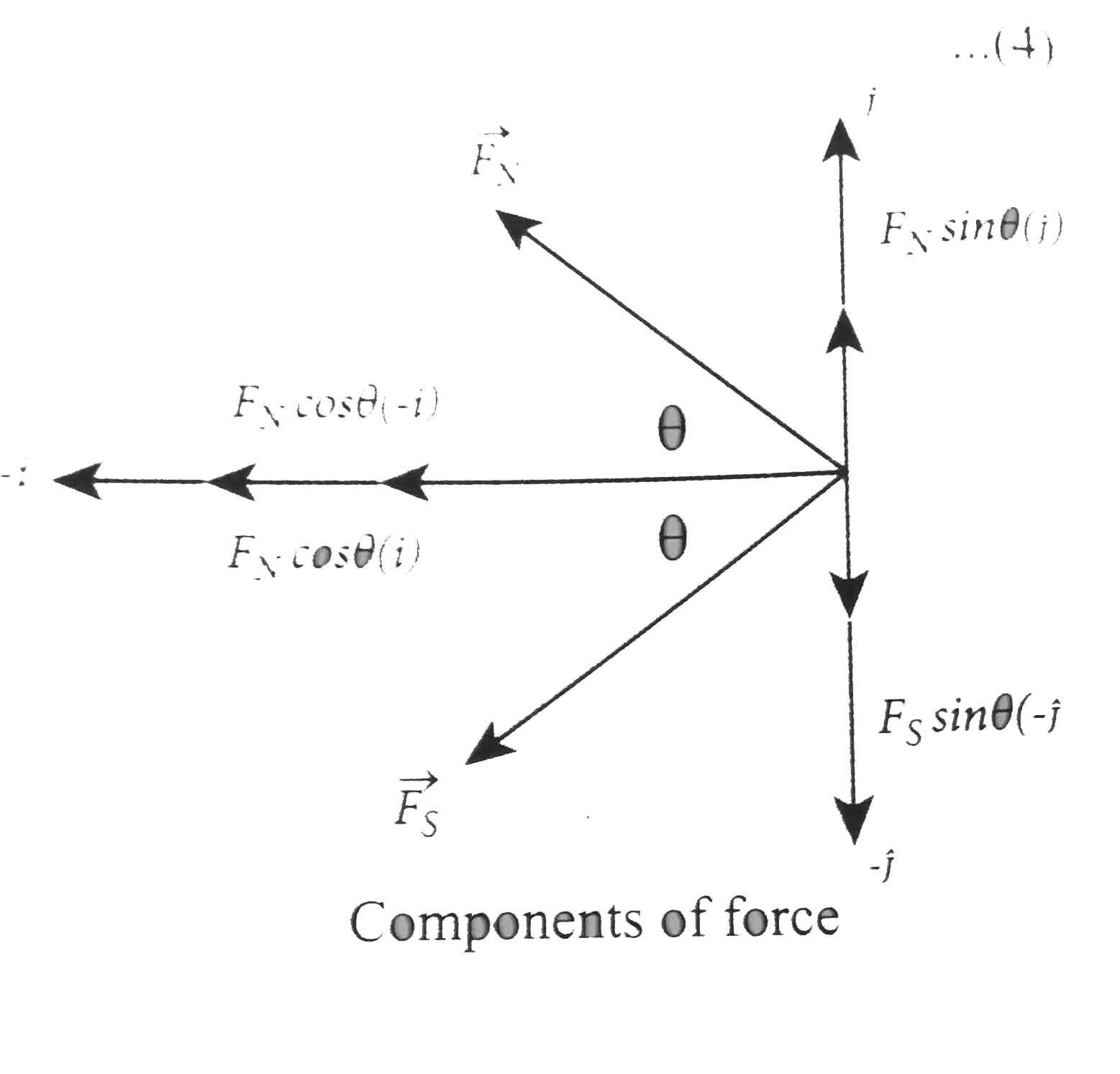
The force of. repulsion between North Pole of the bar magnet and unit north pole at point (in free space) is `vecF=-F_(N)costhetahati+F_(N)sinthetahatj`
Where `F_(N)=(mu_(0)q_(m))/(4pir^(1//2))`
The force of attraction (in free space) between south pole of the bar magnet and unit north pole at point C
`vecs=-F_(S)costhetahati-F_(s)sinthetaj`.......(2)
Where `F_(S)=(mu_(0)q_(m))/(4pir^(1//2))`
From equation (1) and equation (2), the net force at point Cis `vecF=vecF_(N)+F_(s)` . This net force is equal to the magnetic field at the point C.
`vecB=-(2mu_(0))/(4pi)(q_(m))/(r’^(2))costhetahati=-(2mu_(0))/(4pi)(q_(m))/((r^(2)+l^(2))costhetahati`
In a right angle triangle NOC as shown in the Figure 1 `costheta=(adjacent)/(hypotenuse)=(1)/(r’)=(1)/((r^(2)+l^(2))^((1)/(2)))`
Substituting equation 4 in equation 3 we get
`vecB=-(mu_(0)q_(m)xx(2l))/(4pi_((r^(2)+l^(2))^((3)/(2)))hati`......(5)
Since, magnitude of magnetic dipole moment is `|vecP_(m)|=P_(m)=q_(m).2l` and substituting in equation (5), the magnetic field at a point C
`vecB_(equatorial)=-(mu_(0))/(4pi)(P_(m))/((r^(2)+l^(2))^((3)/(2)))hati`......(6)
compared to the distance between geometrical center of bar magnet and the location of point Ci.e.,r>>, then,
`(r^(2)+l^(2))^((3)/(2))=r^(3)`...(7).
Therefore, using equation (7) in equation (6), we get
`vecB_(equatorial)=-(mu_(0))/(4pi)(P_(m))/(r^(3))hati`
Since `P_(m)hati=vecP_(m)`, in general, the magnetic field at equatorial point is given by
`vecB_(equatorial) =-(mu_(0))/(4pi)(P_(m))/(r^(3))`.......(8)
Note that magnitude of Barial is twice that of magnitude of `B_(equatorial)` and the direction of `B_(axial )`and `B_(equatorial)`are opposite.

