Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
FULL MARKS-SAMPLE PAPER-6-PART - III
- Define capacitance . Give its unit.
Text Solution
|
- Distinguish between drift velocity and mobility.
Text Solution
|
- A coil of a tangent galvanometer of diametre 0.24 m has 100 turns. If ...
Text Solution
|
- Mention the way of producing induced emf.
Text Solution
|
- A 400 mH coil of negligible resistance is connected to an AC circuit i...
Text Solution
|
- What are the sign conventions followed for lenses?
Text Solution
|
- Write down the draw backs of Bohr atom model.
Text Solution
|
- What do you mean by leakage current in a diode ?
Text Solution
|
- Distinguish between wireline and wireless communication? Specify the r...
Text Solution
|
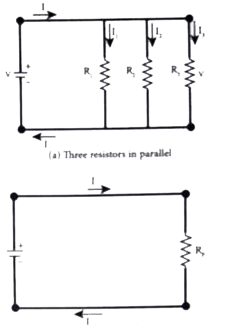
- Explain the equivalent resistance of a series and parallel resistor ne...
Text Solution
|
- Obtain a relation for the magnetic induction at a point along the axis...
Text Solution
|
- Explain the working of a single-phase AC generator with necessary diag...
Text Solution
|
- What is emission spectra? Give their types
Text Solution
|
- Describe the Fizeau's method to determine speed of light.
Text Solution
|
- List out the laws of photoelectric effect.
Text Solution
|
- Describe the structure of nucleus with a suitable diagram.
Text Solution
|
- Explain the working principle of a solar cell. Mention its application...
Text Solution
|
- Elaborate on the basic elements of communication system with the neces...
Text Solution
|