Experimental setup • Wavefronts from `S_(1)` and `S_(2)` spread out and overlapping takes place to the right side of double slit. When a screen is placed at a distance of about 1 meter from the slits, alternate bright and dark fringes which are equally spaced appear on the screen. These are called interference fringes or bands.
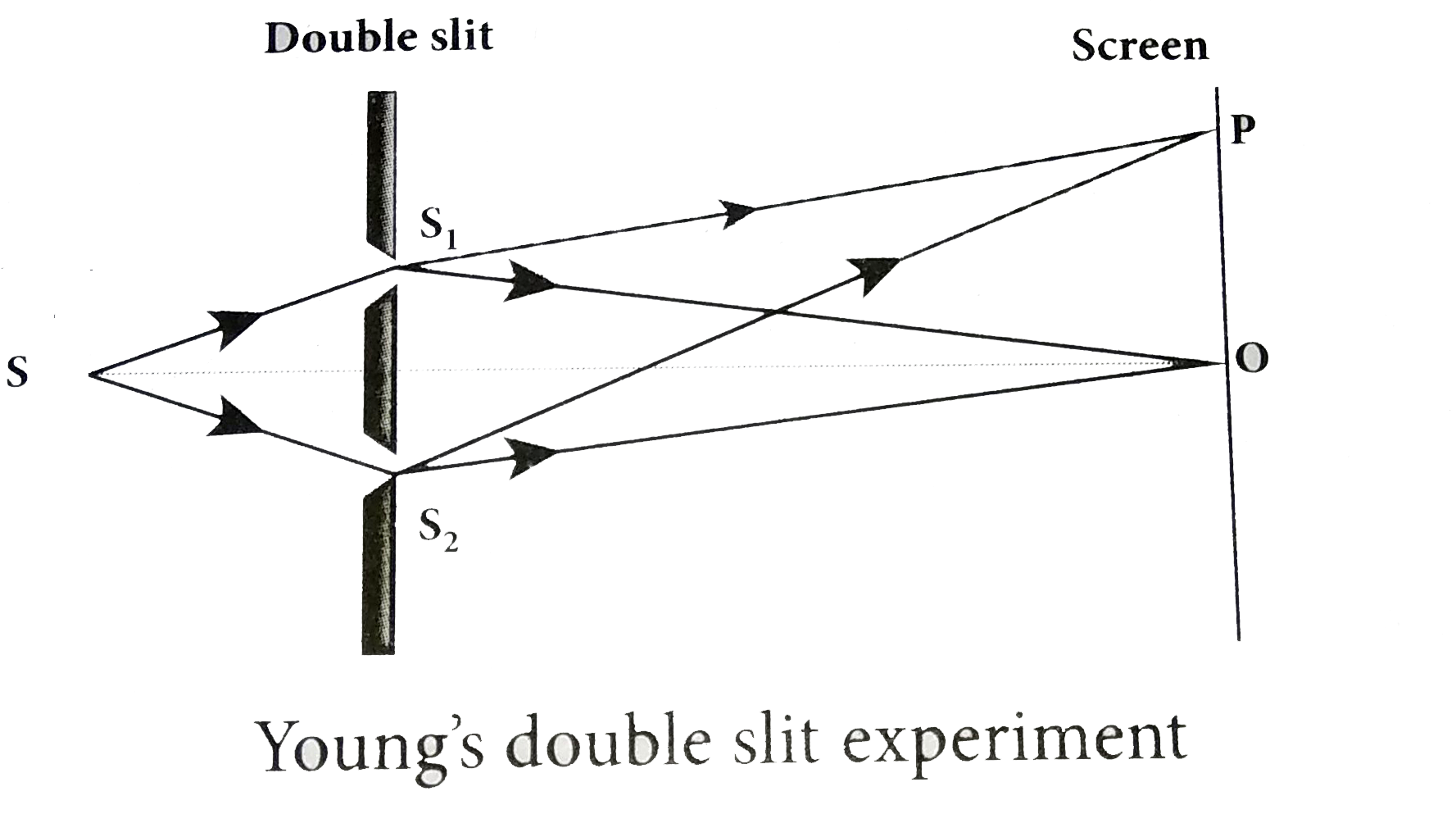
• Using an eyepiece the fringes can be seen directly. At the center point on the screen, waves from `S_(1)` and `S_(2)` travel equal distances and arrive in-phase. These two waves constructively interfere and bright fringe is observed at O. This is called central bright fringe.
• The fringes disappear and there is uniform illumination on the screen when one of the slits is covered. This shows clearly that the bands are due to interference
Equation for path difference • Let d be the distance between the double slits `S_(1)` and `S_(2)` which act as coherent sources of wavelength `lambda` A screen is placed parallel to the double slit at a distance D from it. The mid-point of `S_(1)` and `S_(2)` is C and the midpoint of the screen 0 is equidistant from `S_(1)` and `S_(2)` P is any point at a distance y from O.

• The waves from `S_(1)`and `S_(2)` meet at P either inphase or out-of-phase depending upon the path difference between the two waves.
• The path difference `delta`between the light waves from `S_(1)` and `S_(2)` to the point P is.`delta=S_(2)P-S_(1)P`
• A perpendicular is dropped from the point `S_(1)` to the line `S_(2)` Pat M to find the path difference more precisely. `delta =S_(2)P - MP=S_(2)M`
The angular position of the point P from C is `theta /_OCP = theta`
. From the geometry, the angles `/_OCP` and `/_S_(2)S_(1)`M are equal
.`/_OCP = /_S_(2)S_(1)`M=`theta`
In right angle triangle `triangleS_(1) S_(2) M` the path difference, `S_(2) M` = d sin `thetadelta = d sintheta`
If the angle `theta` is small, sin `theta~~tantheta~~theta` From the right angle triangle `triangleOCP tan theta =(y)/(D)` The path difference, `delta = (dy)/(D)`

