Explain about compound mircoscope and obtain the equation for magnification. Compound microscope:

Explanation

The lens near the object, called the objective, forms a real, inverted, magnified image of the object। This serves as the object for the second lens which is the eyepiece। Eyepiece serves as a simple microscope that produces finally an enlarged and virtual image। The first inverted h. image formed by the objective is to be adjusted close to, but within the focal plane of the eyepiece so that the final image is formed nearly at infinity or at the near point। The final image is Compound microscope inverted with respect to the original object। We can obtain the magnification for a compound microscope.
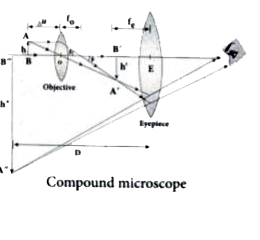Magnification of compound microscope From the ray diagram, the linear magnification due to the objective is,
`m_o=h./(4)`from the figure,tan`beta=h/(f_0)=h./(L)`then
`h./h=l/(f_0),m_o=l/(f_0)`
Here the distance L is between the first focal point of the eyepiece to the second focal point of the objective। This is called the tube length L of the microscope as f, and f, are comparati smaller than L। If the final image is formed at P (near point focusing), the magnincation `m_e` the eyepiece is,
`m_e=1+D/(f_e)`
The total mabnification m in near point focusing is,
`m=m_0m_e=((L)/(f_o))(1+(D)/(f_e))`
If the final image is formed at infinity (normal focusing), the magnification `m_e` of the eyepiece is,
`m_e=D/(f_e)`
The total magnification m in normal focusing is,`m=m_(o)m_(e)=((L)/(f_o))(D/(f_e))`