Consider a bar magnet NS. Let N be the north pole and S be the south pole of the bar magnet, each with pole strength qm and separated by a distance of 21. The magnetic field at a point C (lies along the equatorial line) at a distance r from the geometrical center O of the bar magnet can be computed by keeping unit north pole (`q_(m)C` = 1 A m) at C. The force experienced by the unit north pole at C due to pole strength N-S can be computed using Coulomb’s law of magnetism as follows:
The force of repulsion between North Pole of the bar magnet and unit north pole at point C (in free space) is
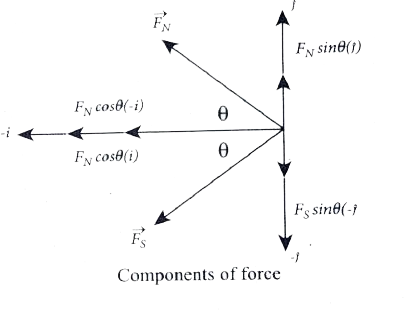
`vec(F)_(N)=-F_(N)costheta hat(i) + F_(N) sintheta hat(j)` ...(1)
Where `F_(N)=(mu_(0)q_(m))/(4pir.^(2))`
The force of attraction (in free space) between south pole of the bar magnet and unit norm pole at point C is
`vec(F)_(s)=-F_(S)costhetahat(i) - F_(s)sinthetaj`
Where `vec(F)_(S)=(mu_(0)q_(m))/(4pir.^(2))`
From equation (1) and equation (2), the net force at point C is `vec(F)=vec(F)_(N) + F_(s)`. This net force is equal to the magnetic field at the point C.
`vec(B)=-(F_(N) + F_(S))costhetahat(i)`
Since `F_(N) = F_(S)`
`vec(B)=(2mu_(0))/(4pi) q_(m)/((r^(2) + l^(2))) costhetahati` ...(3)
In a right angle triangle NOC as shown in the Figure 1
`costheta= ("adjacent")/("hypotenuse")=1/(r.)=1/(r^(2) + l^(2))^(1/2)`...(4)
Substituting equation 4 in equation 3 we get
`vec(B)=-mu_(0)/(4pi) (Q_(M)xx (2L))/(r^(2) + l^(2))^(3/2)` ...(5)
Since, magnitude of magnetic dipole moment is `|vec(P)_(m)|=P_(m)=q_(m).2l` and substituting in equation (5), the magnetic field at a point C is
`vec(B)_("equational")=mu_(0)/(4pi) P_(m)/(r^(2) + l^(2))^(3/2) hati` ...(6)
If the distance between two poles in a bar magnet are small (looks like short magnet) when compared to the distance between geometrical center O of bar magnet and the location of point C i.e., r>> I, then,
`(r^(2) + l^(2))^(3/2)=r^(3)`...(7)
Therefore, using equation (7) in equation (6), we get
`vec(B)_("equational")=mu_(0)/(4pi)P_(m)/r^(3) hati`
Since `P_(m)hat(i)=vec(P)_(m)` , in general, the magnetic field at equitorial point is given by
`vec(B)_("equational")=mu_(0)/(4pi)P_(m)/r^(3)`...(8)
Note that magnitude of `B_("axial")` is twice that of magnitude of `B_("equational")` and the direction of `B_("axial")` and `B_("equational")` are opposite.