Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
FULL MARKS-SAMPLE PAPER -10 (SOLVED)-PART - IV
- Obtain the expression for electric field due to an uniformly charge sp...
Text Solution
|
- Obtain the condition for bridge balance in Wheatstone's bridge.
Text Solution
|
- What is the magnetic field along the axis and equatorial line of a bar...
Text Solution
|
- Give the advantage of AC in long distance power transmission w ith an ...
Text Solution
|
- What is emission spectra? Give their types
Text Solution
|
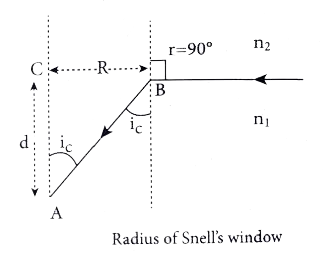
- Obtain the equation for radius of illumination (or) Snell's window.
Text Solution
|
- Explain why photoelectric effect cannot be explained on the basis of w...
Text Solution
|
- Obtain the law of radioactivity. Law of radioactive decay
Text Solution
|
- Explain the construction and working of a full wave rectifier.
Text Solution
|
- Explain the three modes of propagation of electromagnetic waves throug...
Text Solution
|