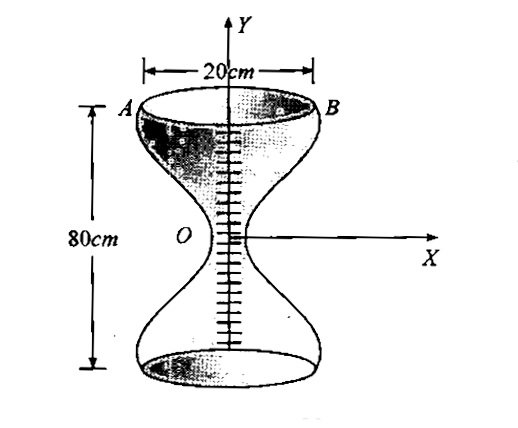Similar Questions
Explore conceptually related problems
Recommended Questions
- A water clock used in ancient Greek is designed as a closed vessel wit...
Text Solution
|
- A water clock consist of a vessel which has a small orifice O. The upp...
Text Solution
|
- A water clock used in ancient Greek is designed as a closed vessel wit...
Text Solution
|
- Water is being poured in a vessel at a constant rate alpha m^(2)//s . ...
Text Solution
|
- What will happen to the water level if the vessel is heated ?
Text Solution
|
- A cylindrical vessel is filled with water upto the height 1 m from the...
Text Solution
|
- A vessel is used to boil water. To boil water faster the thermal condu...
Text Solution
|
- The diameter and height of a narrow cylindrical vessel are 10 cm and 1...
Text Solution
|
- Dimensions of a rectangular vessel 20 cm xx 16 cm xx 11 cm Is, full of...
Text Solution
|