संधारित्र की विद्युत धारिता—किसे संधारित्र की विद्युत धारिता (C) उसे दिए गए आवेश (q) तथा उसके कारण संधारित्र की प्लेटो के बीच विभवान्तर (V) के अनुपात के बराबर होती है।
संधारित्र की धारिता `C= q/V`
फैरड-यदि q = 1 कूलॉम तथा V = 1 वोल्ट तब C= 1 फैरड अत: यदि किसी संधारित्र की प्लेटों को 1 कूलॉम आवेश देने पर उसकी प्लेटों के बीच विभवान्तर 1 वोल्ट हो तब संधारित्र की धारिता 1 फैरड होती है।
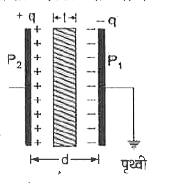
समान्तर प्लेट संधारित्र की धारिता, जब उसकी प्लेटों के बीच आंशिक रूप से परावैद्युतांक रखा हो-माना `P_1` व `P_2` समान्तर प्लेट संधारित्र की दो प्लेटें हैं, जिनके बीच की दूरी d है एवं प्रत्येक प्लेट का क्षेत्रफल A है। माना t मोटाई की परावैद्युत पदार्थ की एक प्लेट संधारित्र की प्लेटों के बीच रखी है। इस प्रकार प्लेटों के बीच (d-t ) मोटाई में वायु तथा t मोटाई में परावैद्युत माध्यम है। प्लेट `P_1` को +q आवेश देने पर प्रेरण के कारण प्लेट `P_2` पर -q आवेश उत्पन्न हो जाता है।
तब प्लेटों के बीच वायु में वैद्युत क्षेत्र की तीव्रता `E_0=q/(epsilon_0A)`
तथा परावैद्युत माध्यम में विद्युत क्षेत्र की तीव्रता E =`q/(K epsilon_0A)`
यदि प्लेटों `P_1` व `P_2` के बीच विभवान्तर V हो, तब
`V=E_0 (d-t) + Et`
`=q/(epsilon_0A)(d-t) + q/(epsilon_0AK)t`
`=q/(epsilon_0 A) [(d-t)+t/K]`
अत: संधारित्र की धारिता `C=q/V=q/(q/(epsilon_0A) [(d-t)+t/K])`
`=(epsilon_0A)/([(d-t) + t/K])`फैरड।
विशेष स्थितियाँ-1. यदि प्लेटों के बीच पूरे स्थान में परावैद्युतांक भरा हो (अर्थात् t = d) तो संधारित्र की धारिता `C=(epsilon_0A)/([(d-d)+d/K])=(Kepsilon_0A)/d` फैरड।
2.यदि प्लेटों के बीच पूरे स्थान में वायु अथवा निर्वात हो ( अर्थात् t=0) तो संधारित्र की धारिता `C=(epsilon_0A)/([(d-0)+0/K])=(epsilon_0A)/d` फैरड।
3. यदि प्लेटों के बीच t मोटाई की धातु की पट्टी हो (K =`oo`) तो संधारित्र की धारिता `C=(epsilon_0A)/([(d-t)+t/oo])=(epsilon_0A)/(d-t)` फैरड।