Text Solution
Verified by Experts
Topper's Solved these Questions
MOTION IN A PLANE
MODERN PUBLICATION|Exercise PRACTICE PROBLEMS (1)|8 VideosMOTION IN A PLANE
MODERN PUBLICATION|Exercise PRACTICE PROBLEMS (2)|9 VideosMECHANICAL PROPERTIES OF FLUIDS
MODERN PUBLICATION|Exercise Chapter Practise Test|16 VideosMOTION IN A STRAIGHT LINE
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST|16 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-MOTION IN A PLANE -Chapter Practice Test
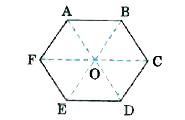
- For a regular hexagon ABCDEF shown below , prove that overset rarr(A...
Text Solution
|
- Can a physical quantity having both magnitude and direction be a vecto...
Text Solution
|
- When the resultant of two vectors is maximum and when minimum ?
Text Solution
|
- A vector is given by vecV=(8.0hati+2.0hatj)m//s . What will be the uni...
Text Solution
|
- A ball is thrown in air . What are its velocity and acceleration at th...
Text Solution
|
- Two bodies of masses 4kg and 6kg are thrown with the same velocity in ...
Text Solution
|
- If |veca+vecb|=|vecas-vecb|, (veca,vecb!=vec0) show that the vectors v...
Text Solution
|
- Find the angle of projection at which horizontal range and maximum hei...
Text Solution
|
- Which is greater , the angular velocity of the hour hand of a watch or...
Text Solution
|
- PROPERTIES OF VECTOR CROSS PRODUCT
Text Solution
|
- Show that the horizontal range is maximum when the angle of projection...
Text Solution
|
- Two balls of masses 2m and 6m are thrown in air : one is vertically u...
Text Solution
|
- Show that there are two angles of projection for which the horizontal ...
Text Solution
|
- Give the relation between linear acceleration and angular acceleration...
Text Solution
|
- A man rides a jet boat with a speed of 40 km//hr in the north -east di...
Text Solution
|
- (a) Show that vector adition is commutative but vector subtraction is ...
Text Solution
|