Text Solution
Verified by Experts
Topper's Solved these Questions
MOTION IN A PLANE
MODERN PUBLICATION|Exercise Revision Exercises (very Short Answer Questions)|46 VideosMOTION IN A PLANE
MODERN PUBLICATION|Exercise Revision Exercises (Additional Questions)|4 VideosMOTION IN A PLANE
MODERN PUBLICATION|Exercise NCERT FILE (Solved) (NCERT (Exemplar Problems Subjective Questions) Very short nswer type questions)|13 VideosMECHANICAL PROPERTIES OF FLUIDS
MODERN PUBLICATION|Exercise Chapter Practise Test|16 VideosMOTION IN A STRAIGHT LINE
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST|16 Videos
MODERN PUBLICATION-MOTION IN A PLANE -Higher Order Thinking Skills & Advanced Level
- A particle is given an initial velocity of vecu=(3 hati+4 hatj) m//s. ...
Text Solution
|
- Magnitudes of the vectors vec A, vec B and vec C are 4, 5 and 3 respec...
Text Solution
|
- If vecP+vecQ=vecR and vecP-vecQ=vecS, prove that vecR^2+vecS^2=2(vecP^...
Text Solution
|
- The resultant of two vectors vec A and vec B is perpendicular to the v...
Text Solution
|
- Find the values of a and b so that vectors vecA and vec B are parallel...
Text Solution
|
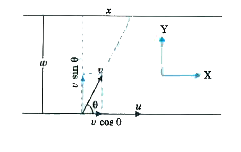
- A man can swim in still water with a speed v . River flows at a speed ...
Text Solution
|