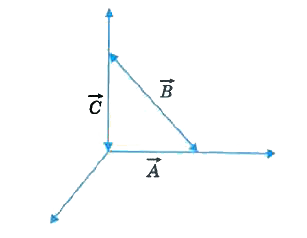
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MOTION IN A PLANE
MODERN PUBLICATION|Exercise Chapter Practice Test|15 VideosMOTION IN A PLANE
MODERN PUBLICATION|Exercise COMPETITION FILE OBJECTIVE TYPE QUESTIONS (INTEGER TYPE QUESTIONS)|10 VideosMECHANICAL PROPERTIES OF FLUIDS
MODERN PUBLICATION|Exercise Chapter Practise Test|16 VideosMOTION IN A STRAIGHT LINE
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST|16 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-MOTION IN A PLANE -COMPETITION FILE OBJECTIVE TYPE QUESTIONS (NCERT (Exemplar Problems Objective Questions))
- The angle between vecA = hati + hatj and vecB = hati - hatj is
Text Solution
|
- Which one of the following statements is true ?
Text Solution
|
- The figure given below shows the orientation of two vectors vecu and v...
Text Solution
|
- The component of a vector r along X-axis will have maximum value if
Text Solution
|
- The range of a projectile fired at an angle of 15^@ is 50 m. If it is ...
Text Solution
|
- Consider the quantities , pressure, power, energy impulse, gravitation...
Text Solution
|
- In a two dimensional motion,instantaneous speed v(0) is a positive con...
Text Solution
|
- In a two -dimensional motion, instantaneous speed vecv(0) is a positiv...
Text Solution
|
- Three vectors vecA,vecB and vecC add up to zero.Find which is false.
Text Solution
|
- It is found that |A+B|=|A|,This necessarily implies.
Text Solution
|
- Two particles are projected in air with speed v(0) at angles theta(1) ...
Text Solution
|
- A particle slides down a frictionless paraboli (y=x^(2)) track (A-B-C)...
Text Solution
|
- Following are four different relations about displacement, velocity an...
Text Solution
|
- For a particle performing uniform circular motion , choose the correct...
Text Solution
|
- For tow vectros vec A and vec B | vec A + vec B| = | vec A- vec B|...
Text Solution
|