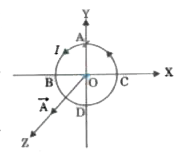
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MOVING CHARGES AND MAGNETISM
MODERN PUBLICATION|Exercise NCERT (Exemplar Problems ) Objective Questions (MCQ Type - II)|5 VideosMOVING CHARGES AND MAGNETISM
MODERN PUBLICATION|Exercise NCERT (Exemplar Problems ) (Very Short Answer Type Questions )|5 VideosMOVING CHARGES AND MAGNETISM
MODERN PUBLICATION|Exercise NCERT FILE (NCERT Additional Exercises)|15 VideosMAGNETISM AND MATTER
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST FOR BOARD EXAMINATION|16 VideosNUCLEI
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST FOR BOARD EXAMINATION|15 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-MOVING CHARGES AND MAGNETISM-NCERT (Exemplar Problems ) Objective Questions (MCQ Type - I)
- Two charged particles traverse identical helical paths in a completely...
Text Solution
|
- Biot-Savart law indicates that the moving electrons (velocity vecv ) p...
Text Solution
|
- A current carrying circular loop of radius R is placed in the x-y plan...
Text Solution
|
- An electron is projected with uniform velocity along the axis of a cur...
Text Solution
|
- In a cyclotron, a charged particle
Text Solution
|
- A circular current loop of magnetic moment M is in an arbitrary orient...
Text Solution
|