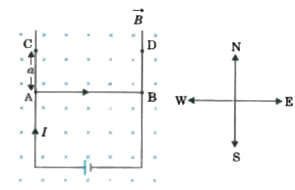
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MOVING CHARGES AND MAGNETISM
MODERN PUBLICATION|Exercise NCERT (Exemplar Problems ) (Very Short Answer Type Questions )|5 VideosMOVING CHARGES AND MAGNETISM
MODERN PUBLICATION|Exercise NCERT (Exemplar Problems ) (Short Answer Type Questions )|6 VideosMOVING CHARGES AND MAGNETISM
MODERN PUBLICATION|Exercise NCERT (Exemplar Problems ) Objective Questions (MCQ Type - I)|6 VideosMAGNETISM AND MATTER
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST FOR BOARD EXAMINATION|16 VideosNUCLEI
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST FOR BOARD EXAMINATION|15 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-MOVING CHARGES AND MAGNETISM-NCERT (Exemplar Problems ) Objective Questions (MCQ Type - II)
- The gyro-magnetic ratio of an electron in an H-atom, according to Bohr...
Text Solution
|
- Consider a wire carrying a steady current, I placed in a uniform magne...
Text Solution
|
- Two identical current carrying coaxial loops, carry current I in an op...
Text Solution
|
- A cubical region of space is filled with some uniform electric and mag...
Text Solution
|
- A charged particle would continue to move with a constant velocity in ...
Text Solution
|