A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
MOVING CHARGES AND MAGNETISM
MODERN PUBLICATION|Exercise COMPETITION FILE (ASSERTION TYPE QUESTIONS)|10 VideosMOVING CHARGES AND MAGNETISM
MODERN PUBLICATION|Exercise COMPETITION FILE (MATRIX MATCH TYPE QUESTIONS)|1 VideosMOVING CHARGES AND MAGNETISM
MODERN PUBLICATION|Exercise COMPETITION FILE (C. MULTIPLE CHOICE QUESTIONS)|28 VideosMAGNETISM AND MATTER
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST FOR BOARD EXAMINATION|16 VideosNUCLEI
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST FOR BOARD EXAMINATION|15 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-MOVING CHARGES AND MAGNETISM-COMPETITION FILE (D. MULTIPLE CHOICE QUESTIONS)
- The magnetic field B inside a long solenoid, carrying a current of 5.0...
Text Solution
|
- There is one infinitely long strip of current with a large width , car...
Text Solution
|
- There is one infinitely long strip of current with a large width , car...
Text Solution
|
- A uniform magnetic field B is applied in a region that is outwards, pe...
Text Solution
|
- A uniform magnetic field B is applied in a region that is outwards, pe...
Text Solution
|
- A uniform magnetic field B is applied in a region that is outwards, pe...
Text Solution
|
- A uniform magnetic field B is applied in a region that is outwards, pe...
Text Solution
|
- In a thin rectangular metallic strip a constant current I flows along ...
Text Solution
|
- In a thin rectangular metallic strip a constant current I flows along ...
Text Solution
|
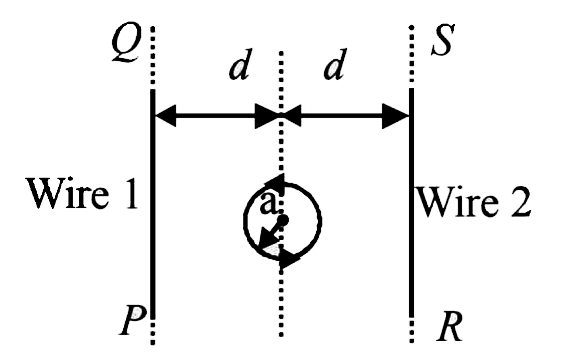
- The figure shows a circular loop of radius a with two long parallel wi...
Text Solution
|