धारावाही चालक से उत्पन्न चुम्बकीय क्षेत्र अर्थात बायो - सावर्ट का नियम - किसी धारावाही चालाक AB के एक अल्पांश `Delta"l` के द्वारा किसी बिन्दु P पर चुम्बकीय क्षेत्र `DeltaB` निम्नलिखित बातों पर निर्भर करता है -
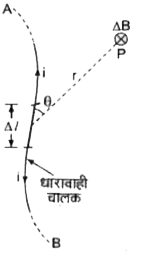
(i) चुम्बकीय क्षेत्र `DeltaB`, चालक में प्रवाहित वैधुत धारा i के अनुक्रमानुपाती होता है।
अर्थात `DeltaBpropi`
(ii) चुम्बकीय क्षेत्र `DeltaB`, चालक के उस अल्पांश की लम्बाई `Delta l` के अनुक्रमानुपाती होता है।
अर्थात `DeltaBpropDeltal`
(iii) चुम्बकीय क्षेत्र `DeltaB`, अल्पांश की लम्बाई तथा अल्पांश को उस बिन्दु P से मिलने वाली रेखा के बीच बनने वाले कोण `theta` की ज्या (sine) के अनुक्रमानुपाती होता है।
अर्थात `DeltaBpropsintheta`
(iv) चुम्बकीय क्षेत्र `DeltaB`, बिन्दु P की अल्पांश से दूरी r के वर्ग के व्यत्क्रमानुपाती होता है।
अर्थात `DeltaBprop1//r^(2)`
इन चारों को मिलाने
`DeltaBprop(iDeltalsintheta)/(r^(2))`
इस सम्बन्ध को ही बायो-सावर्ट नियम कहते है। यदि चालक निर्वात (अथवा वायु) में स्थित हो तो उत्पन्न चुम्बकीय क्षेत्र
`DeltaB=(mu_(0))/(4pi)*(iDeltalsintheta)/(r^(2))`
जहाँ `mu_(0)//4pi` अनुक्रमानुपाती नियतांक है `mu_(0)` को निर्वात की .चुम्बकशीलता. कहते है। इसका मान `4pixx10^(-7)" न्यूटन/ऐम्पियर"^(2)` होता है।
