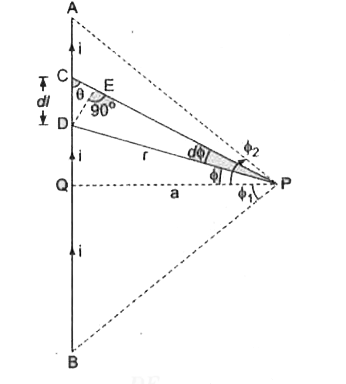
परिमित लम्बाई के सीधे धारावाही चालक के कारण चुम्बकीय क्षेत्र - माना L लम्बाई के एक सीधे चालक AB में i ऐम्पियर की धारा बाह रही है। इस चालक के समीप कोई बिन्दु P है, जहाँ चुम्बकीय क्षेत्र B ज्ञात करना है। बिन्दु P से चालक AB पर लम्ब PQ है जिसकी लम्बाई a है माना चालक AB का अल्पांश भाग CD है जिसकी बिन्दु P से दूरी r तथा `CD=dl` है। माना `angleDPQ=phi` तथा `angleCPD=dphi` | माना `angleDCP=theta` तथा `DE.CP` पर लम्ब है।
बायो - सावर्ट के नियम से, अल्पांश `dl ` के कारण बिन्दु P पर चुम्बकीय क्षेत्र
`dB=(mu_(0))/(4pi)*(idlsintheta)/(r^(2))`
पुनः `DeltaCDE` में, `sin theta=(DE)/(CD)`
अतः `" "DE=cDsintheta=dlsintheta`
`becauseDE`, बिन्दु P पर `dphi` कोण अन्तरित करती है।
`:.dphi` (रेडियन में) `=(DE)/(DP)=(DE)/(r)` अथवा `DE=rdphi`
अतः `alsintheta=rdphi`
तथा `DeltaDPQ` में `cosphi=a/r`, अतः `r=(a)/(cosphi)`
`:." "dB=(mu_(0))/(4pi)*(irdphi)/(r^(2))=(mu_(0))/(4pi)*(idphi)/(r)`
अथवा `dB=(mu_(0))/(4pi)*(icosphidphi)/(a)`
माना `angleBPQ=phi_(1)` तथा `angleAPQ=phi_(2)`
चूँकि `phi_(1)` व `phi_(2)` लम्ब `PQ` से विपरीत दिशाओं में नापे जा रहे है, अतः `phi_(1)` ऋणात्मक व `phi_(2)` धनात्मक होगा |
अतः सम्पूर्ण चालक AB के कारण बिन्दु P पर चुम्बकीय क्षेत्र
`B=int_(-phi_(1))^(phi_(2))(mu_(0))/(4pi)*(icosphidphi)/(a)=(mu_(0))/(4pi)*(i)/(a)int_(-phi_(1))^(phi_(2))=(mu_(0))/(4pi)*i/aint_(-phi_(1))^(phi_(2))cosphi.dphi[because (mu_(0))/(4pi)*i/a=" नियतांक"]`
`=(mu_(0))/(4pi)*i/a[sin phi]_(-phi_(1))^(phi_(2))=(mu_(0))/(4pi)*i/a[sinphi_(2)-sin(-phi_(1))]`
`=(mu_(0))/(4pi)*i/a(sinphi_(1)+sin phi_(2))`
दाएँ हाथ की हथेली के नियम 1 से, चुम्बकीय क्षेत्र B की दिशा कागज़ के तल के लम्बत नीचे की ओर होगी।
विशेष स्थितियाँ -
1. यदि चालक बिन्दु P के दोनों ओर अनन्त दूरी तक जाता है तो
`phi_(1)=phi_(2)=90^(@)`
तब, `B=(mu_(0))/(4pi)*i/a[sin90^(@)+sin90^(@)]`
`=(mu_(0))/(4pi)*(2i)/(a)=(mu_(0))/(2pi)*i/a` न्यूटन/(ऐम्पियर - मीटर) ।
यह अपरिमित लम्बाई के ऋजुरेखीय धारावाही चालक के कारण चुम्बकीय क्षेत्र का सूत्र है।
2. यदि बिन्दु P अपरिमित लम्बाई के चालक के सिरे A के समीप तथा चालक से a दूरी पर है तो `phi_(1)~=pi//2` तथा `phi_(2)~=0`
अतः `B=(mu_(0))/(4pi)*i/a` न्यूटन/(ऐम्पियर - मीटर) ।
