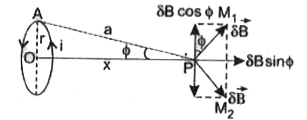वृत्ताकार धारावाही कुण्डली अथवा लूप की अक्ष के अनुदिश चुम्बकीय क्षेत्र - माना r त्रिज्या की एक वृत्ताकार कुण्डली में i धारा प्रवाहित हो रही है माना कुण्डली की अक्ष पर कुण्डली के केन्द्र O से x दूरी पर एक बिन्दु P है जहाँ पर चुम्बकीय क्षेत्र की तीव्रता ज्ञात करनी है (चित्र)। माना कुण्डली अनेक
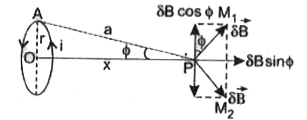
छोटे - छोटे अवयवों से मिलकर बना है इनमे से एक छोटा अवयव A है जो कागज़ के तल के लम्बवत है माना इस अवयव की लम्बाई `deltal` है माना बिन्दु P से इस अवयव A की दूरी a है अतः बायो - सावर्ट के नियम से, बिन्दु P पर चुंबकीय क्षेत्र की तीव्रता
`deltaB=(mu_(0))/(4pi)(ideltalsintheta)/(a^(2))`
परन्तु `deltal` तथा r के बीच कोण `theta=90^(@)` है अतः
`deltaB=(mu_(1))/(4pi)(ideltal)/(a^(2))` (`PM_(1)` दिशा में)
धारा अवयव `ideltal` तथा a के बीच कोण `theta=90^(@)` है अतः
`deltaB=(mu_(0))/(4pi)(ideltal)/(a^(2))` (`PM_(1)` दिशा में)
चुम्बकीय क्षेत्र `deltaB` को अक्ष के अनुदिश व लम्बवत घटको में वियोजित करने पर, लम्बत घटक `deltaBcosphi` परस्पर निरस्त हो जाएंगे जबकि अनुदिश घटक `deltaBsinphi` जुड़ जाएंगे। अतः इनका परिमाण
`BointdBsinphi` परन्तु चित्र से, `sinphi=r/a`
अतः `B=oint(mu_(0))/(4pi)(idl)/(a^(2))xxr/a=(mu_(0))/(4pi)(ir)/(a^(3))ointdl`
परन्तु कुण्डली की लम्बाई `=ointdl=2pir` तथा `a=(r^(2)+x^(2))^(1//2)`
अतः `B=(mu_(0))/(4pi)-(2piir^(2))/((r^(2)+x^(2))^(3//2))=(mu_(0)ir^(2))/(2(r^(2)+x^(2))^(3//2))`
यदि कुण्डली में N फेरे हो तो `B=(mu_(0)Nir^(2))/(2(r^(2)+x^(2))^(3//2))`
चुम्बकीय क्षेत्र B की दिशा कुण्डली की अक्ष के अनुदिश होगी। कुण्डली के केन्द्र पर `x=0` है अतः कुण्डली के केन्द्र पर चुम्बकीय क्षेत्र
`B=(mu_(0)Ni)/(2r)`