बाह्य चुम्बकीय क्षेत्र में स्थित आयताकार धारा लूप पर बल - युग्म का आघूर्ण - माना एक आयताकार लूप ABCD एकसमान बाह्य चुम्बकीय क्षेत्र `vec(B)` में लटकाया गया है (चित्र)। माना लूप की लम्बाई `AB=DC=l` तथा चौड़ाई `AB=BC=b` है
जब किसी धारावाही चालक को चुम्बकीय क्षेत्र में रखते है तो चालक पर एक बल कार्य करने लगता है, जिसकी दिशा फ्लेमिंग के बाएँ हाथ के नियम के अनुसार होती है। जब में .i. धारा दक्षिणावर्त दिशा में प्रवाहित की जाती है तो
(1) लूप की भुजा AB पर बल `F_(1)-ilB` (कागज के तल के लम्बवत ऊपर की ओर) कार्य करता है
(2) लूम की भुजा DC पर बल `F_(2)-ilB` (कागज के तल के लम्बवत नीचे की ओर) कार्य करता है।
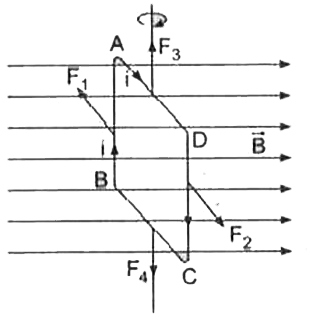
(3) लूप की भुजाएँ AD तथा BC पर लगने वाले बल `F_(3)` व `F_(4)` परस्पर बराबर व विपरीत है तथा इनकी क्रिया - रेखा भी एक ही है, अतः ये दोनों बल एक-दुसरे को निरस्त कर देंगे अर्थात ये बल - युग्म नहीं बनाएँगे।
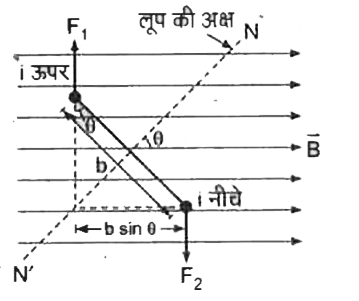
चूँकि बल `F_(1)` व `F_(2)` परिमाण में परस्पर बराबर, दिशा में समान्तर व विपरीत है तथा इनकी क्रिया - रेखाएँ अलग-अलग है अतः ये एक बल - युग्म बनाते है जिसे विक्षेपक बल - युग्म कहते है। इसी बल - युग्म के कारण ही लूप आयताकार अथवा धारावाही अपनी स्थिति से घूमने लगता है।
माना किसी क्षण लूप अक्ष (लूप के तल पर खींचा गया अभिलम्ब `"NN".` ) चुम्बकीय क्षेत्र B की दिशा से `theta` कोण बनाती है (चित्र), तब विक्षेपक बल - युग्म का आघूर्ण
`tau =` बल `xx` लम्ब-दूरी `=ilBxxbsintheta`
परन्तु `lxxb=A` (लूप का क्षेत्रफल)
अतः `tau-iABsintheta` . . . (1)
यदि एक लूप के स्थान पर, N लूपों से बनी कोई कुण्डली अथवा परिनालिका हो तो पूरी कुण्डली पर लगने वाले बल-युग्म का आघूर्ण
`tau=NiABsintheta` . . . (2)
यदि `theta=90^(@)` तब कुण्डली पर लगने वाले बल - युग्म का आघूर्ण
`tau=NiAB`
चुम्बकीय द्विध्रुव आघूर्ण - धारा लूप पर कार्यरत बल आघूर्ण,
`tau=iABsintheta`
`=MBsintheta`
जहाँ `M=iA`, धारा लूप का चुम्बकीय द्विध्रुव आघूर्ण है। यदि `theta=90^(@)` तब
`tau_("max")=MB`
यदि `B=1" वेबर/मीटर"^(2)`, तब
`tau_("max")=M`
अतः धारा लूप का चुम्बकीय द्विध्रुव आघूर्ण उस पर कार्यरत अधिकतम बल आघूर्ण के बर्बर होता है जबकि वह एकांक तीव्रता के चुम्बकीय क्षेत्र में लंबवत स्थित हो।
दिया है : `A=1.00" सेमी"^(2)=1.00xx10^(-4)" मीटर"^(2)`
`I=2` ऐम्पियर
धारा लूप का चुम्बकीय द्विध्रुव आघूर्ण,
`M=iA`
`=2xx1.0xx10^(-4)`
`=2xx10^(-4)" ऐम्पियर - मीटर"^(2)` |

