Similar Questions
Explore conceptually related problems
Recommended Questions
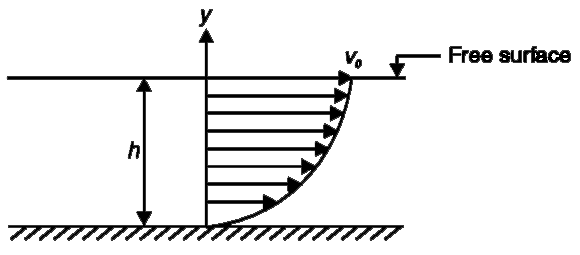
- A liquid is flowing through a horizontal channel. The speed of flow (v...
Text Solution
|
- In dimension of circal velocity v(0) liquid following through a take a...
Text Solution
|
- A particle is dropped from some height. After falling through height h...
Text Solution
|
- A ball is dropped from a height h onto a floor and rebounds to a heigh...
Text Solution
|
- A liquid is flowing through a horizontal channel. The speed of flow (v...
Text Solution
|
- During a painting process, a thin, flat tape of width b (dimension per...
Text Solution
|
- A liquid is flowing through a horizontal channel. The speed of flow (v...
Text Solution
|
- Two holes are made at depths h and 2h from the top. A liquid of densit...
Text Solution
|
- Two holes are made at depths h and 2h from the top. A liquid of densit...
Text Solution
|