एक अध्यापिका दो सेक्शनों के विद्यार्थियों के प्रदर्शनों का विश्लेषण 100 अंक की गणित की परीक्षा लेकर करना चाहती है । उनके प्रदर्शनों को देखने पर वह यह पति है की केवल कुछ ही विद्यार्थियों के प्राप्तांक 20 से कम है और कुछ विद्यार्थियों के प्राप्तांक 70 या उससे अधिक हैं । अतः, उसने विद्यार्थियों को 0-20, 20-30,..., 60-70, 70-100 जैसे विभिन्न माप वाले अंतरालों में वर्गीकृत करने का निर्णय लिया । तब उसने निम्नलिखित सारणी बनाई ।
किसी विद्यार्थी ने इस सारणी का एक आयतचित्र बनाया, जिसे आकृति 14.4 में दिखाया गया है ।

इस आलेखीय निरूपणकी जाँच सावधानी से कीजिए । क्या आप समझते हैं की यह आलेख आकंड़ों का सही-सही निरूपण करता है? इसका उत्तर हैः नहीं । यह आलेख आंकड़ों का एक गलत चित्र प्रस्तुत है । जैसा की हम पहले बता चुके हैं आयतों के क्षेत्रफल आयतचित्र की बारम्बारताओं के समानुपाती होते हैं । पहले इस प्रकार के प्रश्न हमारे सामने नहीं उठे थे, क्योंकि सम्भि आयतों की चौडाईयाँ सामान थी । परन्तु, क्योंकि यहाँ आयतों की चौडाईयाँ बदल रही हैं, इसलिए ऊपर दिया गया आयतचित्र आकंड़ों का एक सही-सही चित्र प्रस्तुत नहीं करता । उदहारण के लिए, यहाँ अंतराल 60 -70 की तुलना में अंतराल 70-100 की बारंबारता अधिक है ।
अतः आयतों की लम्बाइयों में कुछ परिवर्तन (modifications) करने की आवश्यकता होती है, जिससे की क्षेत्रफल पुनः बारम्बारताओं की समानुपाती हो जाये ।
इसके लिए निम्नलिखित चरण लागु करने होते हैः
1. न्यूनतम वर्ग चौड़ाई वाला एक वर्ग अंतराल लीजिए । ऊपर के उदाहरण में, न्यूनतम वर्ग चौड़ाई 10 है ।
2. तब आयतों की लम्बाइयों में इस प्रकार परिवर्तन कीजिए जिससे की वह वर्ग चौड़ाई 10 के समानुपाती हो जाये ।
उदाहरण की लिए, जब वर्ग चौड़ाई 20 होती है, तब आयत की लम्बाई 7 होती है । अतः जब वर्ग चौड़ाई 10 हो, तो आयत की लम्बाई `(7)/(20) xx 10 = 3.5` होगी ।
एक प्रक्रिया को लागू करते रहने पर, हमें निम्नलिखित सारणी प्राप्त होती हैः
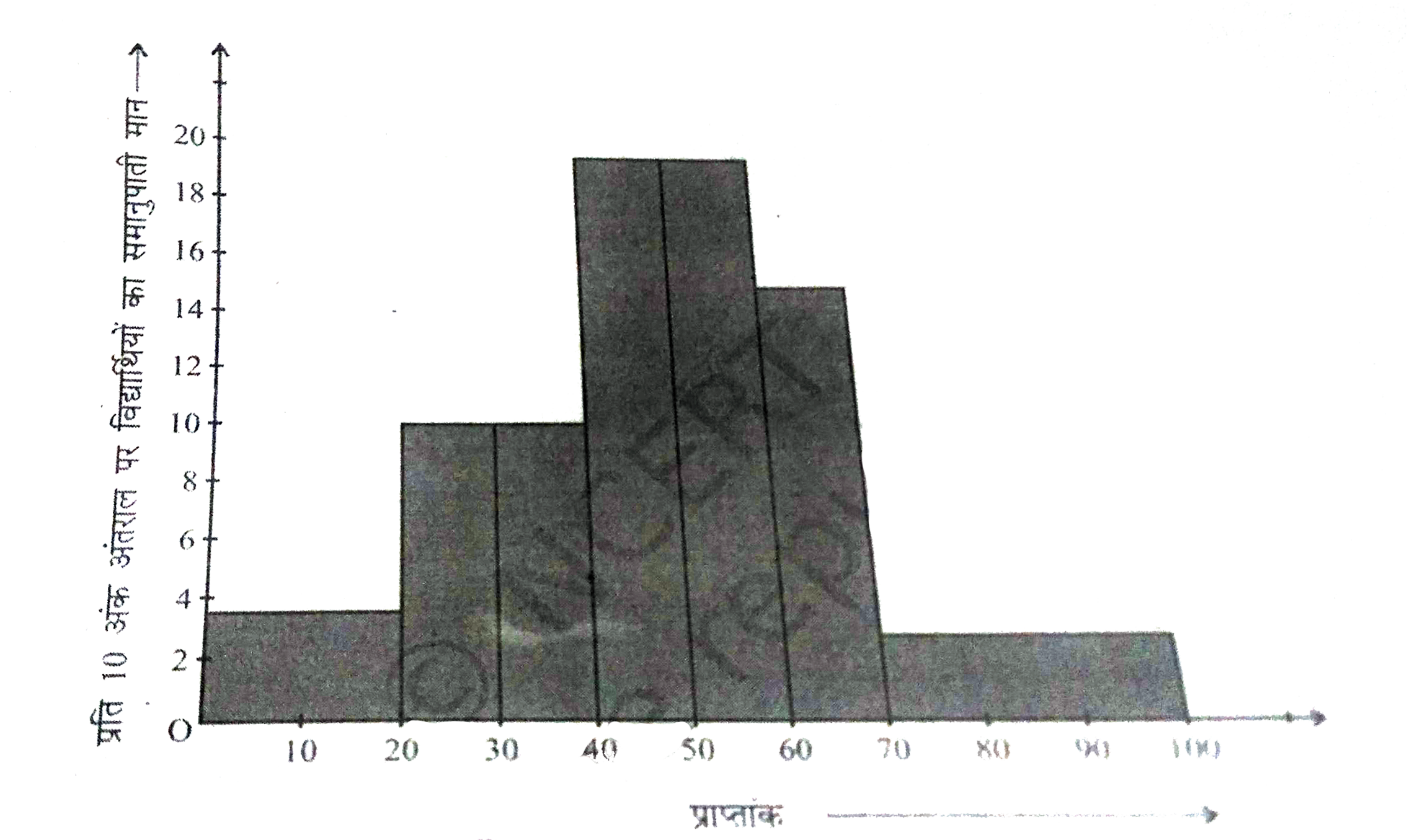
क्योंकि हमने प्रत्येक स्थिति में 10 अंकों के अंतराल पर ये लम्बाईयाँ परिकलित की हैं, इसलिए आप यह देख सकते हैं की हम इन लम्बाइयों को 'प्रति 10 अंक अंतराल पर विद्यार्थियों के समानुपाती मान' सकते है ।
परिवर्ती चौड़ाई वाला सही आयतचित्र आकृति 14.5 में दिखाया गया है ।