व्यक्तिकरण प्रकाश तरंगो के अध्यारोपण की घटना है। इसकी निम्नलिखित है - (i) प्रकाश एकवर्णी होना चाहिए (ii) कम्पन विस्तार समान होना चाहिए (iii) प्रकाश स्त्रोत कला - सम्बद्ध होना चाहिए तथा (iv) को संकीर्ण होना चाहिए।
व्यक्तिकरण की घटना को प्रदर्शित करने के लिए फ्रेसनेल ने द्विक - प्रिज्म का प्रयोग किया। इसकी मदद से किसी प्राथमिक एकवर्णी प्रकाश - स्त्रोत के दो कला सम्बद्ध स्त्रोत प्राप्त किये जा सकते है यह दो प्रिज्मों के संयोग से बनता है जिनके अपवर्तक कोण काफी छोटे एक (लगभग 30 मिनट) होते है। इनके आधार एक दूसरे के संपर्क में रहते है इस कारण इनका एक कोण करीब `179^(@)` होता है।
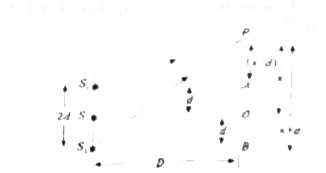
जब इसको एकवर्णी प्रकाश स्त्रोत के समक्ष रखा जाता है तो अपवर्तन के बाद `S_(1)` तथा `S_(2)` से आती प्रतीत होती है। यानि `S_(1)` तथा `S_(2)` S का आभासी प्रतिबिम्ब है जो कला सम्बद्ध होते है अतः इनसे निर्गत प्रकाश तरंगो का अध्यारोपण होता है जिसके फलस्वरूप पर्दे पर व्यक्तिकरण। फ्रिन्जें प्राप्त होती है
पथान्तर `=S_(2)P-S_(1)P`

अब चित्र से, `(S_(1)P)^(2)=D^(2)+(x-d)^(2)` तथा `(S_(2)P)^(2)=D^(2)+(x+d)^(2)`
अब `(S_(2)P)^(2)-(S_(1)P)^(2)=(x+d)^(2)-(x-d)^(2)`
या `(S_(2)P-S_(1)P)(S_(2)P+S_(1)P)=x^(2)+d^(2)+2xd-x^(2)-d^(2)+2xd`
या `(S_(2)P-S_(1)P)(4xd)/((SP+SP))`
यदि OP काफी काम हो तो `S_(1)P=S_(2)P=D` अतः पथान्तर `(4xd)/(D+D)=(2xd)/(D)`
संपोषी व्यक्तिकरण के लिए, पथान्तर `=(2xd)/(D)=nlamda,x=n(Dlamda)/(2d)`
यदि n वें एवं `(x+1)` वें फ्रिन्ज की दूरी क्रमशः `x_(n)` तथा `x_(n+1)` हो तो फ्रिन्ज की चौड़ाई
`(beta)=x_(n+1)-x_(n)((n+1)Dlamda)/(2d)-(nDlamda)/(2d)=(Dlamda)/(2d)lamda=(2 beta d)/(D)`
`:.` यदि `beta`, d एवं D मालूम हो तो `lamda` का मान ज्ञात किया जा सकता है
इसी प्रकार विनाशी व्यक्तिकरण में भी `lamda=(2 beta d)/(D)` ही प्राप्त होता है
फ्रिन्ज की चौड़ाई का व्यंजक - समीकरण (i) की सहायता से ही संपोषी व्यक्तिकरण के `beta=(Dlamda)/(2 d)` लिए एवं विनाशी व्यक्तिकरण के लिए भी `beta=(Dlamda)/(2 d)`
यानी दीप्त एवं अदीप्त दोनों प्रकार की फ्रिन्जो की चौड़ाई समान होती।
यदि D = स्त्रोत की पर्दे से दूरी, `lamda=` प्रक्षा तरंग का तरंगदैर्घ्य
`2d=` कला सम्बद्ध स्त्रोतों के बीच की दूरी, मालूम हो तो फ्रिन्ज की चौड़ाई ज्ञात जा सकती है।

