Home
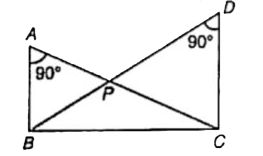
Class 14
MATHS
DeltaABC and DeltaDBC have a common base...

`DeltaABC and DeltaDBC` have a common base and drawn towards one sides. `angleBAC = angleBDC = 90^(@)`. If AC and DB intersect at P, then:

A

`APxxPC=BPxxPD`

B

`APxxBP=PCxxPD`

C

`APxxPD=PCxxBP`

D

none of these

Text Solution

Verified by Experts

The correct Answer is:
A
Promotional Banner

Topper's Solved these Questions

  • GEOMETRY

    ARIHANT SSC|Exercise EXERCISE(LEVEL 1)|54 Videos

  • GEOMETRY

    ARIHANT SSC|Exercise EXERCISE(LEVEL 2)|52 Videos

  • GEOMETRY

    ARIHANT SSC|Exercise INTRODUCTORY EXERCISE - 12.4|10 Videos

  • FUNDAMENTALS

    ARIHANT SSC|Exercise TEST OF YOU - LEARNING - 2|40 Videos

  • HCF AND LCM

    ARIHANT SSC|Exercise Exercise Higher Skill Level Questions|18 Videos

Similar Questions

Explore conceptually related problems

DeltaABC and DeltaDBC are on the same base BC but on opposite sides of it. AD and BC intersect each other at O. If AO=a cm, DO=b cm and the area of DeltaABC=x cm^(2) , then what is the area (in cm^(2) ) of DeltaDBC ?

Two triangles BACandBDC, right angled at Aand D respectively,are drawn on the same base BC and on the same side of BC. If AC and DB intersect at P, prove that APxPC=DPxPB.

In DeltaABC,angleB=90^(@). If P is the mid-point of side AC, then PA=PB=

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that DeltaABD~=DeltaACD

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that DeltaABP~=DeltaACP

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to BP intersect BC at P, show that AP bisects angleA as well as angleD .

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see figure). If AD is extended to intersect BC at P, show that : (i) DeltaABD cong DeltaACD (ii) DeltaABP cong DeltaACP (iii) AP bisects angleA as well as angleD (iv) AP is the perpendicular bisector of BC.

DeltaABC and DeltaDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC. If AD is extended to intersect BC at E, show that (i) DeltaABD ~=DeltaACD (ii) DeltaABE~=DeltaACE (iii) AE bisects angleA as well as angleD (iv) AE is the perpendicualr bisector of BC.

Slove the following questions. In the figure, DeltaADB and DeltaCDB are drawn on the same base BD.if AC and BD intersect at O, then prove that (A(DeltaADB))/(A(DeltaCDB)) = (AO)/(CO).

ARIHANT SSC-GEOMETRY-INTRODUCTORY EXERCISE - 12.5
  1. In the above figure , O is the centre of the circle, AB and CD are dia...

    Text Solution

    |

  2. The quadrilateral formed by the bisectors of the angles of a parallelo...

    Text Solution

    |

  3. DeltaABC and DeltaDBC have a common base and drawn towards one sides. ...

    Text Solution

    |

  4. In the given figure, angleBAC and angleBDC are the angles of same segm...

    Text Solution

    |

  5. In the given figure, O is the centre of the clrcle. angleABO = 60^(@)....

    Text Solution

    |

  6. In the figure ,find the value of x.

    Text Solution

    |

  7. In the adjoining figure, O is the centre of the circle and D angleOBD ...

    Text Solution

    |

  8. In the given figure, DeltaABC is an equilateral triangle. Find angleBE...

    Text Solution

    |

  9. In the given figure, AB is the diameter of the circle. Find the value ...

    Text Solution

    |

  10. In the given figure, ABCD is a cyclic quadrilateral and diagonals D bi...

    Text Solution

    |

  11. In the given figure, ABCD is a cyclic quadrilateral and AB is diameter...

    Text Solution

    |

  12. In the given figure, angleCOB = 40^(@), AB is the diameter of the circ...

    Text Solution

    |

  13. In the given figure, O is the centre of circle. angleAOC = 120^(@). F...

    Text Solution

    |

  14. In the given figure, O is the centre of the circle and angleAOC = 100^...

    Text Solution

    |

  15. In the given figure, O is the centre of circle, angleAOB =100^(@). Fin...

    Text Solution

    |

  16. In the given figure, AB is the diameter of the circle, angleADC = 120^...

    Text Solution

    |

  17. In the given figure, O is the centre of the circle. angleAOB = 70^(@),...

    Text Solution

    |

  18. In the given figure, angleCAB = 40^(@) and angleAKB = 105^(@). Find an...

    Text Solution

    |

  19. In the given figure, ABC is an isosceles triangle in which AB = AC and...

    Text Solution

    |

  20. In the given figure, AB is the diameter. angleBAD = 70^(@)and angleDBC...

    Text Solution

    |