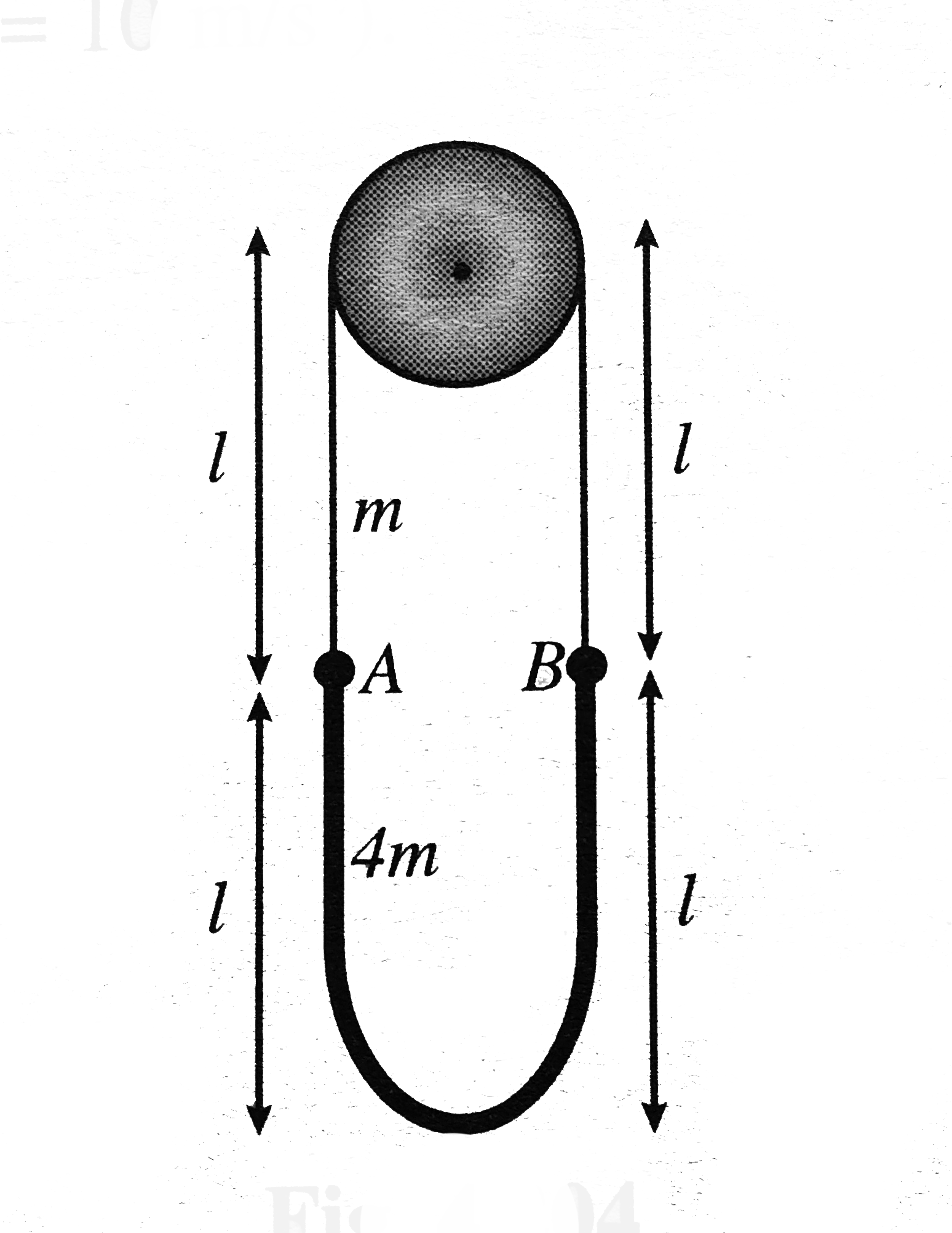Similar Questions
Explore conceptually related problems
Recommended Questions
- Two uniform ropes having linear mass densities m and 4m are joined to ...
Text Solution
|
- A uniform thin rod is bent in the form of closed loop ABCDEFA as shown...
Text Solution
|
- Two uniform ropes having linear mass densities m and 4m are joined to ...
Text Solution
|
- In a closed loop, which has some inductance but negligible resistance,...
Text Solution
|
- A uniform thin rod is bent in the form of closed loop ABCDEFA as shown...
Text Solution
|
- A uniform rope of linear mass density lambda (kg/m) passes over a smoo...
Text Solution
|
- Two masses M and M/ 2 are joint together by means of a light inextensi...
Text Solution
|
- A rope of mass 5 kg is hanging between two supports as shown. The tens...
Text Solution
|
- A circular loop placed in uniform B is transformed into elliptical loo...
Text Solution
|