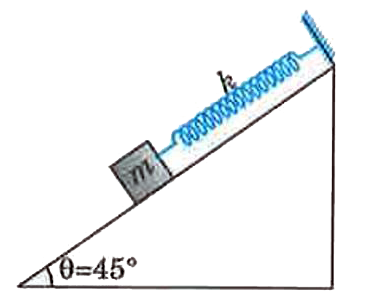
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
OSCILLATIONS
MODERN PUBLICATION|Exercise Competition ASSERTION REASON TYPE QUESTIONS|10 VideosOSCILLATIONS
MODERN PUBLICATION|Exercise Practice Test (For Board Examination)|12 VideosOSCILLATIONS
MODERN PUBLICATION|Exercise Competition File (MATRIX MATCH TYPE QUESTIONS)|2 VideosMOTION IN A STRAIGHT LINE
MODERN PUBLICATION|Exercise CHAPTER PRACTICE TEST|16 VideosPHYSICAL WORLD
MODERN PUBLICATION|Exercise Revision exercises (Long answer questions)|6 Videos
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-OSCILLATIONS -Competition (INTEGER TYPE QUESTIONS)
- A particle is executing simple harmonic motion under the action of a f...
Text Solution
|
- A spring of unstretched length 40 cm and spring constant k is attached...
Text Solution
|
- The maximum seperation between two particles executing simple harmonic...
Text Solution
|
- A simple pendulum of time period of oscillation 2.0 s is suspended ver...
Text Solution
|
- A simple pendulum suspended vertically from a rigid support is moving ...
Text Solution
|
- A particle executes a linear simple harmonic motion of amplitude 20 cm...
Text Solution
|
- The figure shows a mass M attached to a series arrangement of two spri...
Text Solution
|
- A block of mass m is suspended from a spring fixed to the ceiling of a...
Text Solution
|
- Two simple harmonic motions are represented by the equations y(1) = ...
Text Solution
|
- A mass of 0.2 kg, length 1m and cross sectional area 4.9 xx 10^(-7) m^...
Text Solution
|