Home
Class 12
PHYSICS
The field potentail in a certain region...

The field potentail in a certain region of space depends only on the `x` coordinate as `varphi = -ax^(2) + b`, where `a` and `b` are constants. Find the distribution of the space charge `rho (x)`.

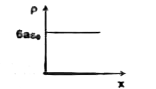
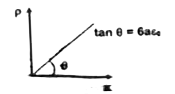
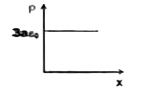
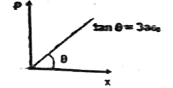
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
B
Promotional Banner

Topper's Solved these Questions

  • PHYSICS PART2

    FIITJEE|Exercise Section (I) : Subjective|4 Videos

  • PHYSICS PART2

    FIITJEE|Exercise Section (II) : MCQ|27 Videos

  • PHYSICS PART-III

    FIITJEE|Exercise NUMERICAL BASED QUESTIONS DECIMAL TYPE|11 Videos

  • ROTATIONAL MECHANICS

    FIITJEE|Exercise COMPREHENSION - IV|2 Videos

Similar Questions

Explore conceptually related problems

The field potentail in a certain region of space depends only on the x coordinate as varphi = -ax^(3) + b , where a and b are constants. Find the distribution of the space charge rho (x) .

Let f(x) =ax^(2) -b|x| , where a and b are constants. Then at x = 0, f (x) is

Find the partial fractions of (ax+b)/((x-1)^(2)) , where a and b are constants.

Let f(x)=ax^(2)-b|x| , where a and b are constant . Then at x=0 , f(x) has

FInd the derivative by first principle ax+b where a and b are constants

A partical of mass m is located in a unidimensionnal potential field where potentical energy of the partical depends on the coordinates x as U (x) = (A)/(x^(2)) - (B)/(x) where A and B are positive constant. Find the time period of small oscillation that the partical perform about equilibrium possition.

The potential energy of a particle depends on its x-coordinates as U=(Asqrt(x))/(x^2 +B) , where A and B are dimensional constants. What will be the dimensional formula for A/B?

A particle of mass m is present in a region where the potential energy of the particle depends on the x-coordinate according to the expression U=(a)/(x^2)-(b)/(x) , where a and b are positive constant. The particle will perform.

The electric field strength depends only on the x and y coordinates according to the law E = a (x i + yj) (x^(2) + y^(2)) , where a is a constant , i and j are the unit vectors of the x and y axes. Find the flux of the vector E through a sphere of raidus R with its centre at the origin of coordinates.

A particles is in a unidirectional potential field where the potential energy (U) of a partivle depends on the x-coordinate given by U_(x)=k(1-cos ax) & and 'a' are constant. Find the physical dimensions of 'a' & k.