Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
MODERN PUBLICATION-WORK, ENERGY AND POWER -Chapter Practice Test
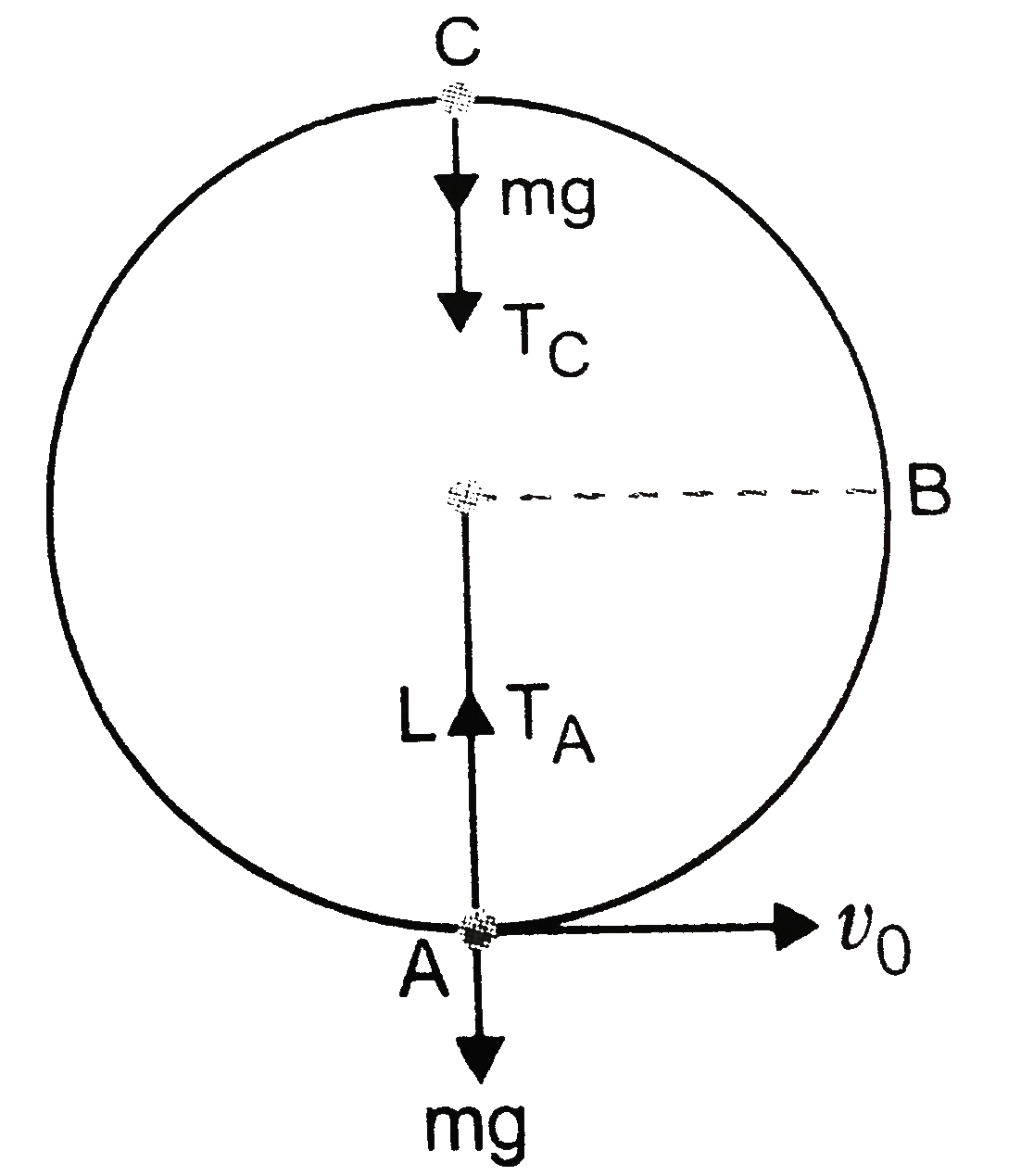
- A bob of mass m is suspended by a light string of length L. It is impa...
Text Solution
|
- Is work done by a non conservative force always negative ? Comment.
Text Solution
|
- When is KE of a planet revolving around the sun maximum?
Text Solution
|
- What is the work done by centripetal force in moving a body throug...
Text Solution
|
- What will happen to potential energy of a spring when it is compres...
Text Solution
|
- What will happen to the K.E oa a body if its momentum is doubled ?
Text Solution
|
- A light body and a heavy body have same linear momentum. Which one has...
Text Solution
|
- Two springs A and B are identical to each other . The spring A is h...
Text Solution
|
- If the momentum of a body is increased by 50%, then what will be the p...
Text Solution
|
- Can a body have momentum without energy?
Text Solution
|
- A bus of mass 1500 kg is accelerating from to rest to a velocity of...
Text Solution
|
- EXPRESSION FOR GRAVITATIONAL POTENTIAL ENERGY
Text Solution
|
- State and prove work - energy theroem .
Text Solution
|
- A ball of mass 0.1 kg is thrown vertically with a speed of 7 " m ...
Text Solution
|
- Prove that the energy remains constant in case of a freely falling bod...
Text Solution
|
- Obtain graphically and mathematically work done by a variable force.
Text Solution
|
- Discuss briefly the elastic collision in one dimension . Also , analys...
Text Solution
|