Similar Questions
Explore conceptually related problems
Recommended Questions
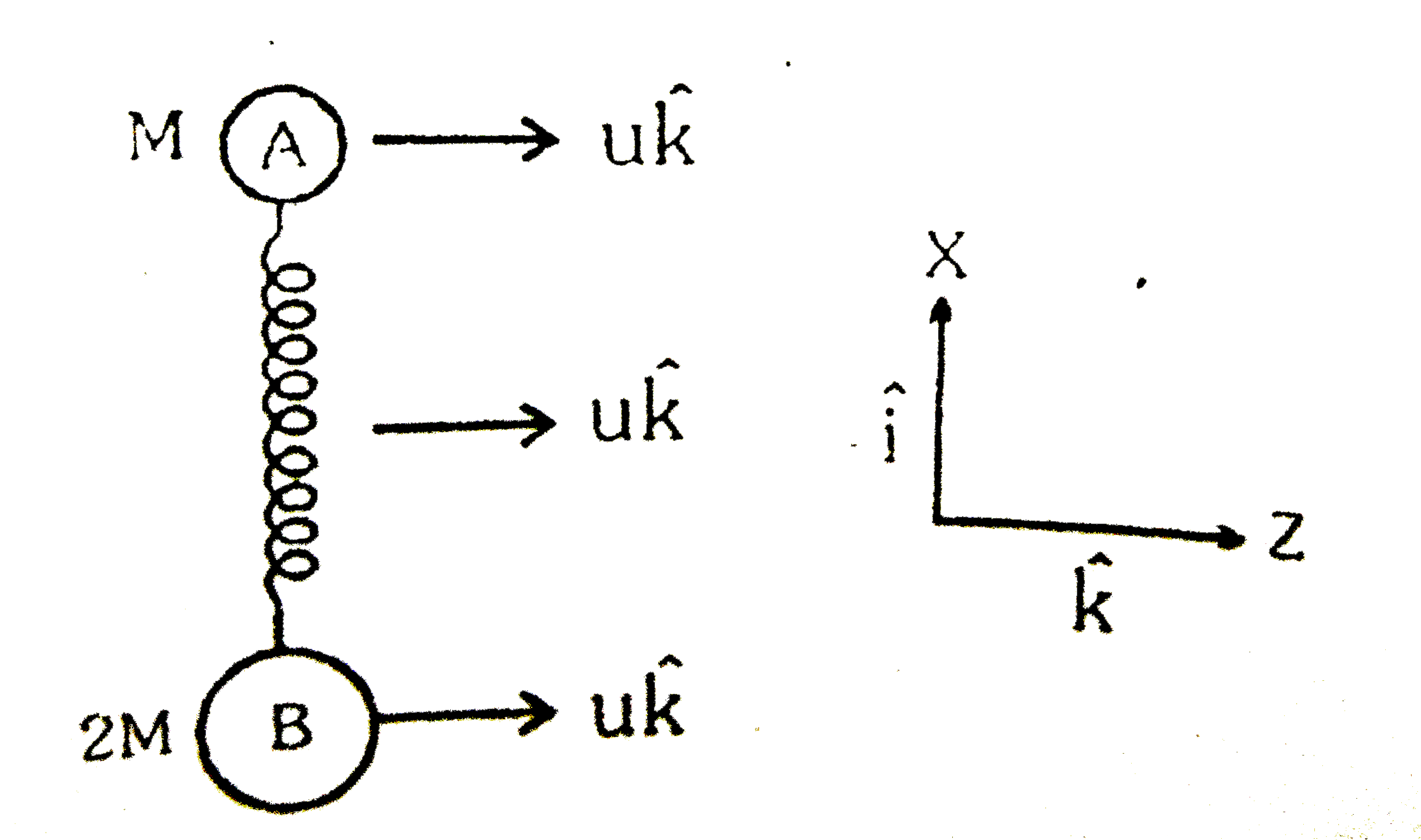
- Two masses A and B of mass M and 2M respectively are connected by a co...
Text Solution
|
- Two blocks A and B of masses m and 2m respectively are placed on a smo...
Text Solution
|
- An ideal spring is permanently connected between two blocks of masses ...
Text Solution
|
- Consider the system shown below, with two equal masses m and a spring ...
Text Solution
|
- Two masses A and B of mass M and 2M respectively are connected by a co...
Text Solution
|
- A system consists of block A and B each of mass m connected by a light...
Text Solution
|
- Two ring of mass m and 2m are connected with a light spring and can sl...
Text Solution
|
- Two blocks A and B of the same mass are connected to a light spring an...
Text Solution
|
- Two blocks of masses m and m' are connected by a light spring on a hor...
Text Solution
|