हाइजेन के तरंग सिद्धांत - हाइजेन के तरंग सिद्धांत के अनुसार किसी प्रकाश स्रोत से प्रकाश चारों तरफ तरंग के रूप में समान गति से फैलती है। तरंग के प्रत्येक बिंदु का फेज समान होता है। इसे आरंभिक तरंग कहा जाता है यह तरंग किसी वस्तु से टकराने पर ऊर्जा स्थानान्तरित करती है तथा टक्कर का बिंदु एक नया श्रोत बन जाता है, जिससे नई तरंग की उत्पत्ति होती है। इस तरंग को द्वितीय तरंग कहा जाता है। इस प्रकार ऊर्जा का संचरण माध्यम में तरंग के रूप में होता है। यही हाइजेन का तरंग सिद्धांत है।
परावर्तन के नियम का सत्यापन - माना कि एक समतल तरंग एक समतल सतह पर आपतित होती है। मान कि आपतित तरंग का एक भग OP है जो सतह AB को बिन्दु O पर मिलती है। समय t = 0 पर बिन्दु O द्वितीय प्रकाश स्रोत का काम करता है तथा इससे निकलने वला द्वितीय तरंग नियत वेग v से चारों ओर फैलते हैं। बिन्दु P पर से आपतित तरंग सतह AB को t समय में बिन्दु O से चला द्वितीय तरंग चलकर सतह O. `O_(2)` को छूती है लेकिन बिन्दु `O_(2)` से निकला तरंग t समय के अन्त में वहीं पर है क्योंकि उसको फैलने का समय नहीं मिला है। अगर आपतित समतल तरंग OP के किसी भी भाग से चसला कम्पन सतह AB से मिलने के बाद सतह `O.O_(2)` को t समय के अन्त में छूती है तो `O.O_(2)` को परावर्तित तरंग कहा जायेगा। सतह OP पर लम्ब आपतित किरण को दिखाती है। माना कि बिन्दु C से चला कम्पन सतह AB को बिन्दु `O_(1)` पर `t_(1)` समय के बाद छूती है तथा `O_(1)` से चला कम्पन `t_(2)` समय के बाद `O.O_(2)` को बिन्दु Q पर छूती है। अगर `t_(1)+t_(2)` का मान t के बराबर हो, तो `O.O_(2)` परावर्तित तरंग माना जायेगा।
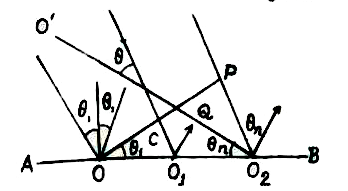
`Delta OO_(2)P` तथा `OO_(1)C` से `(PO_(2))/(CO_(1))=(V*t)/(V*t_(1))=(OO_(2))/(OO_(1))`
या, `(t_(1))/(t)=(OO_(1))/(OO_(2))=(OO_(2)-O_(1)O_(2))/(OO_(2)) " "...(i)`
`Delta P^(1)O O_(2)` तथा `QO_(1) Q_(2)` से, `(OP.)/(Q_(1)Q)=(V*t)/(V*t_(2))=(OO_(2))/(O_(1)O_(2))`
या, `(t_(2))/(t)=(O_(1)O_(2))/(OO_(2))" " ...(ii)`
समी. (i) तथा (ii) से `(t_(1))/(t)=1-(t_(2))/(t)` या `(t_(1)+t_(2))/(t)=1`, या, `t_(1)+t_(2)=1`
अत: `PO_(2)` परावर्तित समतल तरंग है।
पुन: `Delta POO_(2)` से, `sin theta_(i)=(PO_(2))/(OO_(2))=(V*t)/(OO_(2))`
या `V*t=OO_(2)sin theta_(i) " " ...(iii)`
`Delta P.O O_(2)` से `sin theta_(r)=(OP.)/(OP_(2))=(V*t)/(OO_(2))`
या `V*t=O O_(2)sin theta_(r )" " ...(iv) `
समी. (iii) और (iv) `" " OO_(2)sin theta_(i)=O O_(2)sin theta_(r ) therefore theta_(i)=theta_(r )`
आपतन कोण = परावर्तन का कोण, अत: परावर्तन का पहला नियम सत्यापित हुआ।
तथा आपतित किरण अभिलम्ब तथा परावर्तित किरण एक ही बिंदु O पर मिलते हैं। अत: व एक ही सतह पर हैं। अत: परावर्तन का दूसरा नियम सत्यापित होता है।
अपवर्तन के नियम का सत्यापन - माना XY सीमारेखा पर कोई समतल आपतित तरंगाग्र AB है। XY सीमारेखा दो माध्यम जिनके अपवर्तन गुणांक `n_(1)` तथा `n_(2)(n_(2) gt n_(1))` है जिसमें प्रकाश का वेग क्रमश: `V_(1)` और `V_(2)` है। हाइजेंस के सिद्धान्तानुसार, समतल तरंगाग्र AB का प्रत्येक बिंदु नये विक्षोभ श्रोत की तरह कार्य करता है जैसा कि नीचे चित्र में दिखाया गया है।
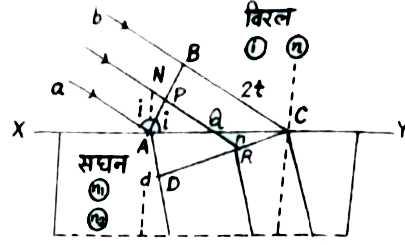
समय t के पश्चात तरंगाग्र AB की स्थिति सघन माध्यम में तरंगाग्र CD के द्वारा दी जाती है। CD वास्तविक अपवर्तित तरंगात्र होगा यदि आपतित तरंगाग्र के किसी भी बिंदु (माना P) से उत्पन्न द्वितीयक तरंगिकाएँ बिंदु Q से होते हुए तरंगाग्र CD के बिंदु R तक पहुँचती है।
द्वितीय तरंगिका के PQR तक पहुँचने में लिया गया समय,
`t=(PQ)/(V_(1))=(QR)/(V_(2))" " ...(i)`
`DeltaPQR` से, `sin i=(PQ)/(AQ)` या, `PQ=AQ sin i" "...(ii)`
QCR से, `sin r=(QR)/(QC)` या, `QR=QC sin r`
या, `QR=(AC-AQ)sin r" " ...(iii)`
समी. (ii) और (iii) के मान समी. (i) में रखने पर
`t=(AQ sin i)/(V_(1))+((AC-AQ)sin r)/(V_(2))=AQ((sin i)/(V_(1))-(sin r)/(V_(2)))+(AC sin r)/(V_(2))`
यह समय बिन्दु Q की स्थिति पर निर्भर नहीं करता, इसलिए `AQ ((sin i)/(V_(1))-(sin r)/(V_(2)))` शून्य होगा।
या, `=AQ ((sin i)/(V_(1))-(sin r)/(V_(2)))=0`, या, `(sin i)/(V_(1))=(sin r)/(V_(2))` या, `(sin i)/(sin r)=(V_(1))/(V_(2))`
निर्वात् में प्रकाश के वेग C से दाई ओर गुण व भाग करने पर,
`(sin i)/(sin r)=(C xx V_(1))/(C xx V_(2))=[(C )/(V_(2))][(C )/(V_(1))]`
`=(n_(2))/(n_(1))=n " " (sin i)/(sin r)=n` इस प्रकार अपवर्तन के नियम का सत्यापित होता है।

