Similar Questions
Explore conceptually related problems
Recommended Questions
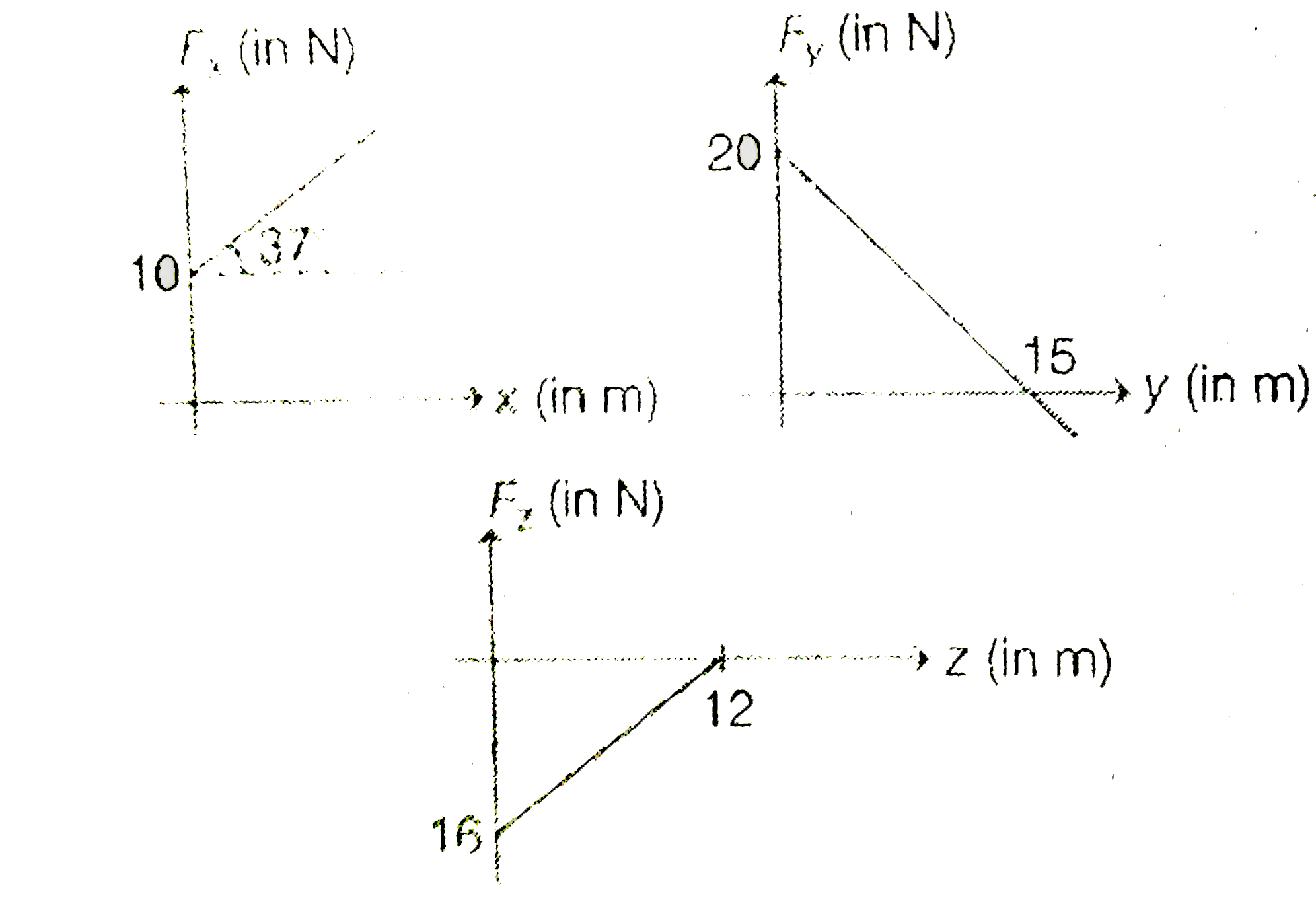
- Three components of a force acting on a particle are varying according...
Text Solution
|
- A force F = -K(y hatI + x hatj) (where K is a posive constant ) acts o...
Text Solution
|
- A force F=-K(yhati+xhatj) (where K is a positive constant) acts on a p...
Text Solution
|
- Graphs shows the acceleration of a 3 kg particle as an applied force m...
Text Solution
|
- A force F=-K(yhati+xhatj) (where K is a positive constant) acts on a p...
Text Solution
|
- A force vecF(yhatl+xhatJ), where K is a positive constant, acts on a p...
Text Solution
|
- Three components of a force acting on a particle are varying according...
Text Solution
|
- A force vecF=(4hati+5hatj)N acts on a particle moving in XY plane. Sta...
Text Solution
|
- X-Y-तल में गतिमान एक कण पर एक बल vecF = -k(y hati + x hatj) (जहाँ k एक...
Text Solution
|