A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
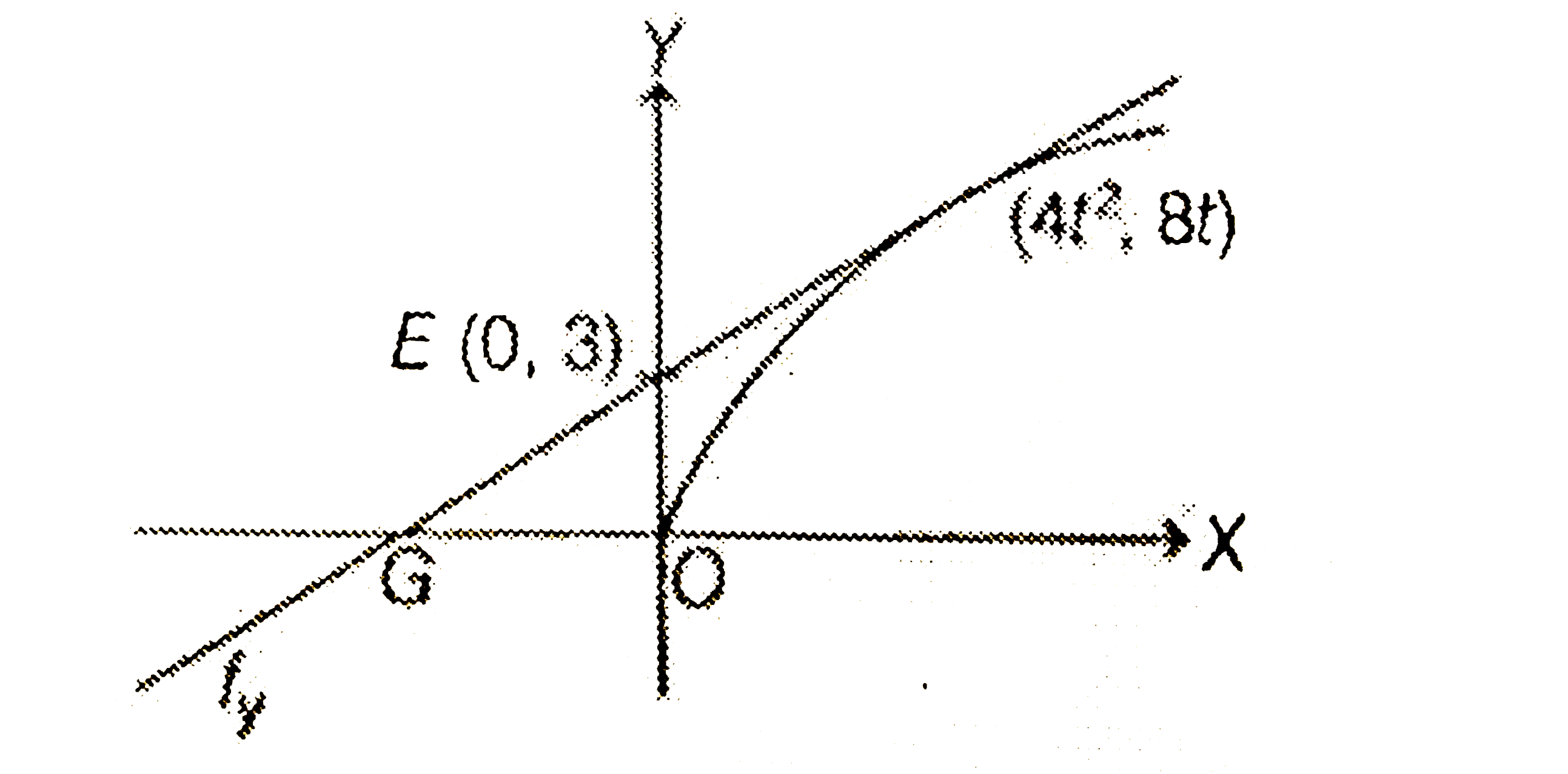
- A line L : y = mx + 3 meets y-axis at E (0, 3) and the arc of the para...
Text Solution
|
- A line L : y = mx + 3 meets y-axis at E (0, 3) and the arc of the para...
Text Solution
|
- Let the line y = mx intersects the curve y^2 = x at P and tangent to y...
Text Solution
|
- Let a line y = mx ( m gt 0) intersect the parabola, y^2 = 4x at a po...
Text Solution
|
- line L:y=mx+3 meets y–axis at E(0, 3) and the are of the parabola y^(2...
Text Solution
|
- Let a line y=mx(m>0 ) intersect the parabola y^(2) =x at a point "P"...
Text Solution
|
- एक रेखा L:y=mx+3,y अक्ष के बिन्दु E(0, 3) तथा परवलय के चाप y^(2)=16x, ...
Text Solution
|
- For a curve y=f(x) slope of tangent at (x0,y0) is given by
Text Solution
|
- A line L : y = mx + 3 meets y-axis at E (0, 3) and the arc of the para...
Text Solution
|