A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
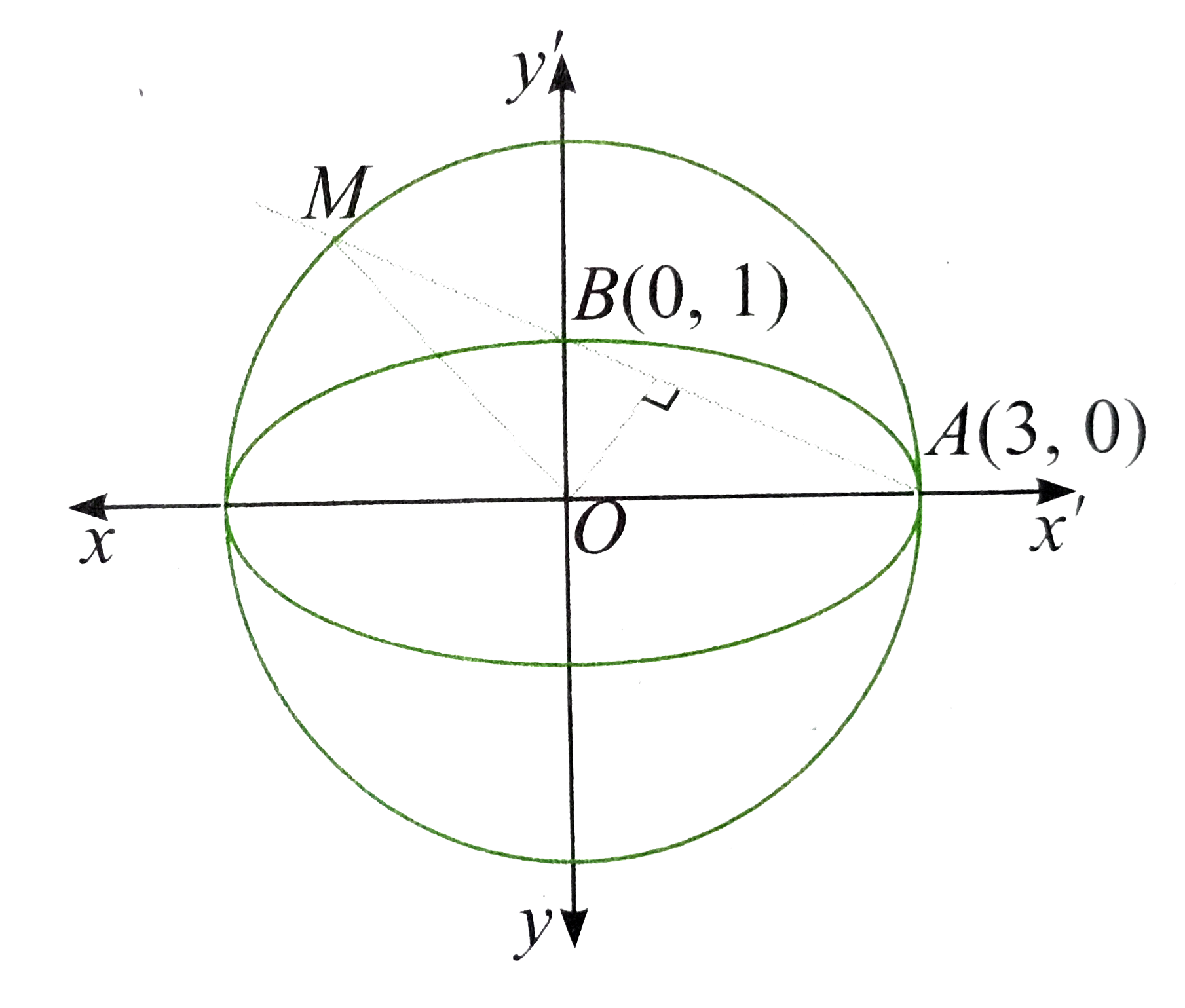
- The line passing through the " extremity "A" of the major axis and ex...
Text Solution
|
- The line passing through the extremity A of the major exis and extremi...
Text Solution
|
- In an ellipse,if the lines joining focus to the extremities of the min...
Text Solution
|
- The line passing through the extremity A of the major axis and extremi...
Text Solution
|
- दीर्घवृत्त x^(2) + 9y^(2) = 9 के दीर्घ अक्ष के शीर्ष A व लघु अक्ष के ...
Text Solution
|
- The line passing through the " extremity "A" of the major axis and ex...
Text Solution
|
- The line passing through the extremity A of major axis and extremity B...
Text Solution
|
- The line passing through the extremity A of the major exis and extremi...
Text Solution
|
- The line passing through the extremity A of the major axis and extremi...
Text Solution
|