Similar Questions
Explore conceptually related problems
Recommended Questions
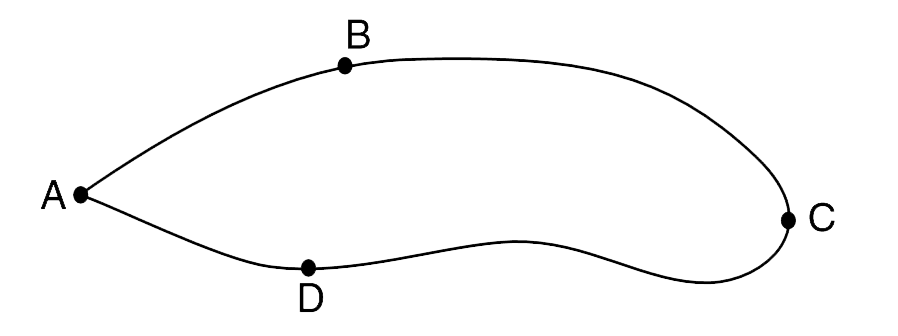
- A particle moves along the loop A–B–C–D–A while a conservative force a...
Text Solution
|
- If W(1) W(2) and W(3) represent the work done in moving a particle fro...
Text Solution
|
- A particle moves along the loop A–B–C–D–A while a conservative force a...
Text Solution
|
- One mole of an ideal gas is taken from a to b along two paths denoted ...
Text Solution
|
- A particle is moving in a conservative force field from point A to poi...
Text Solution
|
- In position A kinetic energy of a particle is 60 J and potential energ...
Text Solution
|
- The work done in moving a particle in the gravitational field of earth...
Text Solution
|
- In forcd oscillation of a particle, the amplitude is maximum for a fre...
Text Solution
|
- A particle is moving in a conservative force field from point A to poi...
Text Solution
|