Similar Questions
Explore conceptually related problems
Recommended Questions
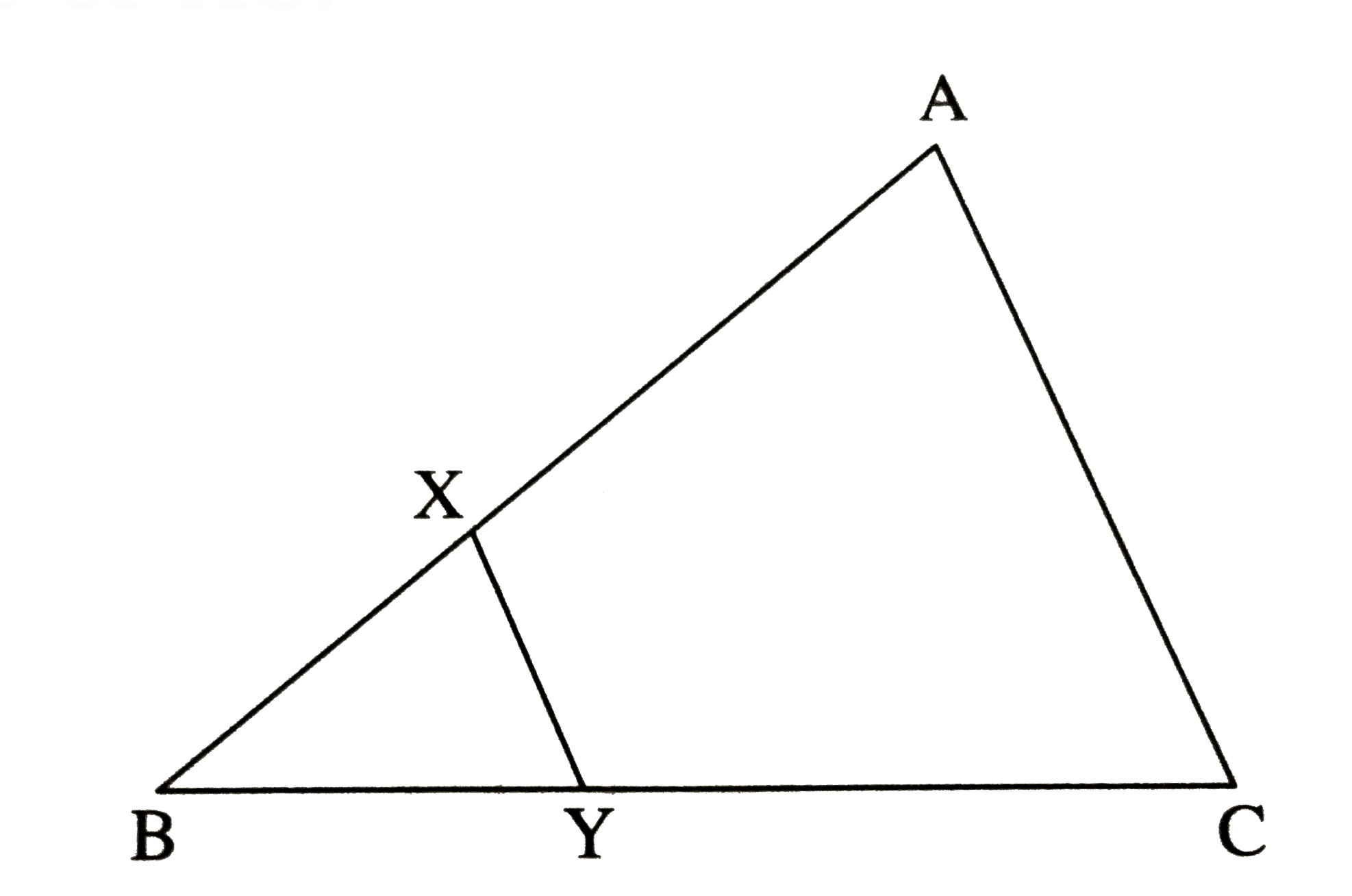
- In figure XY|| seg AC. If 2AX=3BX and XY=9, complete the activity to f...
Text Solution
|
- The value of |[a,a+d,a+2d] , [a+d,a+2d,a+3d] , [a+2d,a+3d,a+4d]|+|[b,b...
Text Solution
|
- वर्ग समतलीय संकर [Pt(NH(3))(Br)(Cl)py]^(0) के लिए ज्यामितीय समावयवों क...
Text Solution
|
- In Delta ABC, P,Q and R are midpoints of sides AB,AC and BC respectiv...
Text Solution
|
- In figure XY|| seg AC. If 2AX=3BX and XY=9, complete the activity to f...
Text Solution
|
- If triangleABC ~ triangleXYZ then complete the following brackets. (AB...
Text Solution
|
- In the adoining figure, XY abs() seg AC. If 2 AX = 3 BX and XY = 9, fi...
Text Solution
|
- In the adjoining figure , XY || seg AC . If 2AX = 3 xxBX and XY=9. Co...
Text Solution
|
- The correct order of size among Br^(+), Br, Br^(-)
Text Solution
|