Similar Questions
Explore conceptually related problems
Recommended Questions
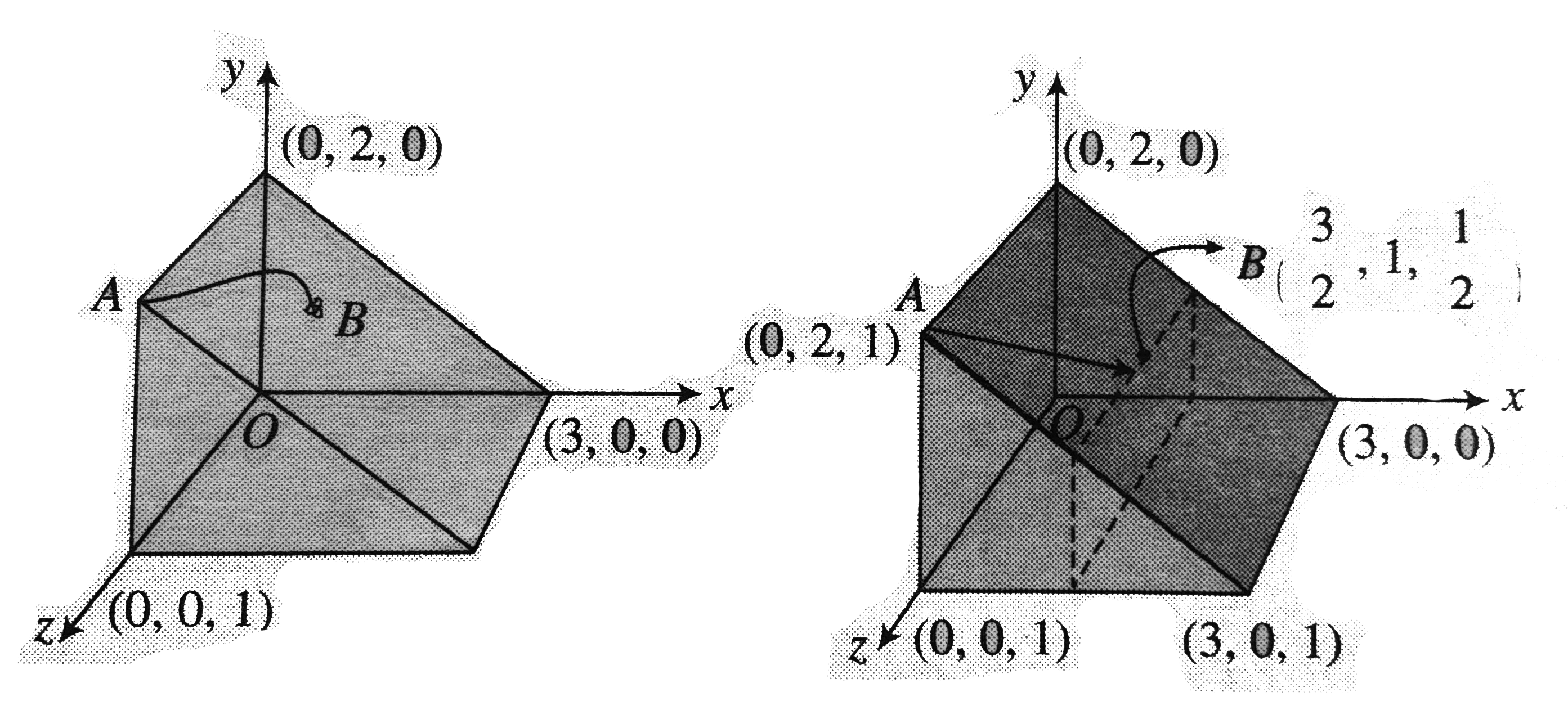
- An insect crawls from A to B where B is the centre of the rectangular ...
Text Solution
|
- An insect crawls from A to B where B is the centre of the rectangular ...
Text Solution
|
- A disc is rotating with constant angular velocity omega in anticlockw...
Text Solution
|
- Biological name of insect (vector) carrying the plague
Text Solution
|
- Insects of genus Phlebotomus are vectors for disease
Text Solution
|
- Vector insects are which
Text Solution
|
- Write names of any two insect vectors.
Text Solution
|
- A lizard, at an initial distance of 21 cm behind an insect, moves fro...
Text Solution
|
- Diseases that are spread through insect vectors
Text Solution
|
 .
.