Similar Questions
Explore conceptually related problems
Recommended Questions
- The work done by the force = vec F = A (x^(2) hati + 2 x^(2) hatj), wh...
Text Solution
|
- A body is displaced from prigin to (1m,1m) by force F=(2yhati + 3x^(2)...
Text Solution
|
- A body is displaced from (0,0) to (1 m, 1m) along the path x = y by a ...
Text Solution
|
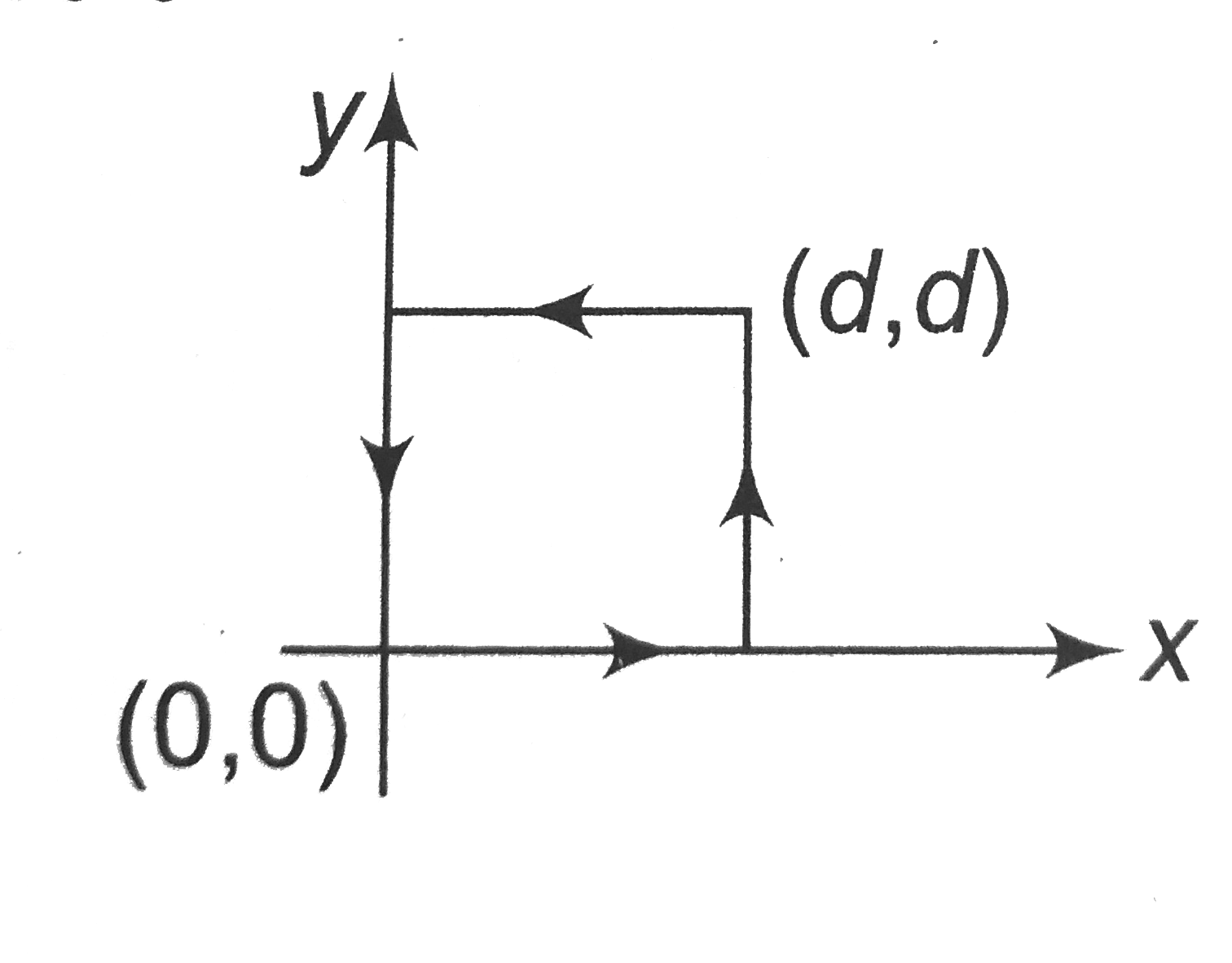
- A particle is movbed from (0, 0) to (a, a) under a force F =(x^(2)hati...
Text Solution
|
- The work done by the force vec(F)=A(y^(2) hati+2x^(2)hatj) , where A i...
Text Solution
|
- If vec r = 3 hati + 2 hatj - 5 hatk , vec a= 2 hati - hatj + hatk, ve...
Text Solution
|
- एक बल F =2x एक कण पर X -अक्ष के अनुदिश कार्यरत है, जहाँ F न्यूटन में ...
Text Solution
|
- Work done around a path closed by a constant force
Text Solution
|
- Calculate the work done if a particle displaces through ( 2 h...
Text Solution
|