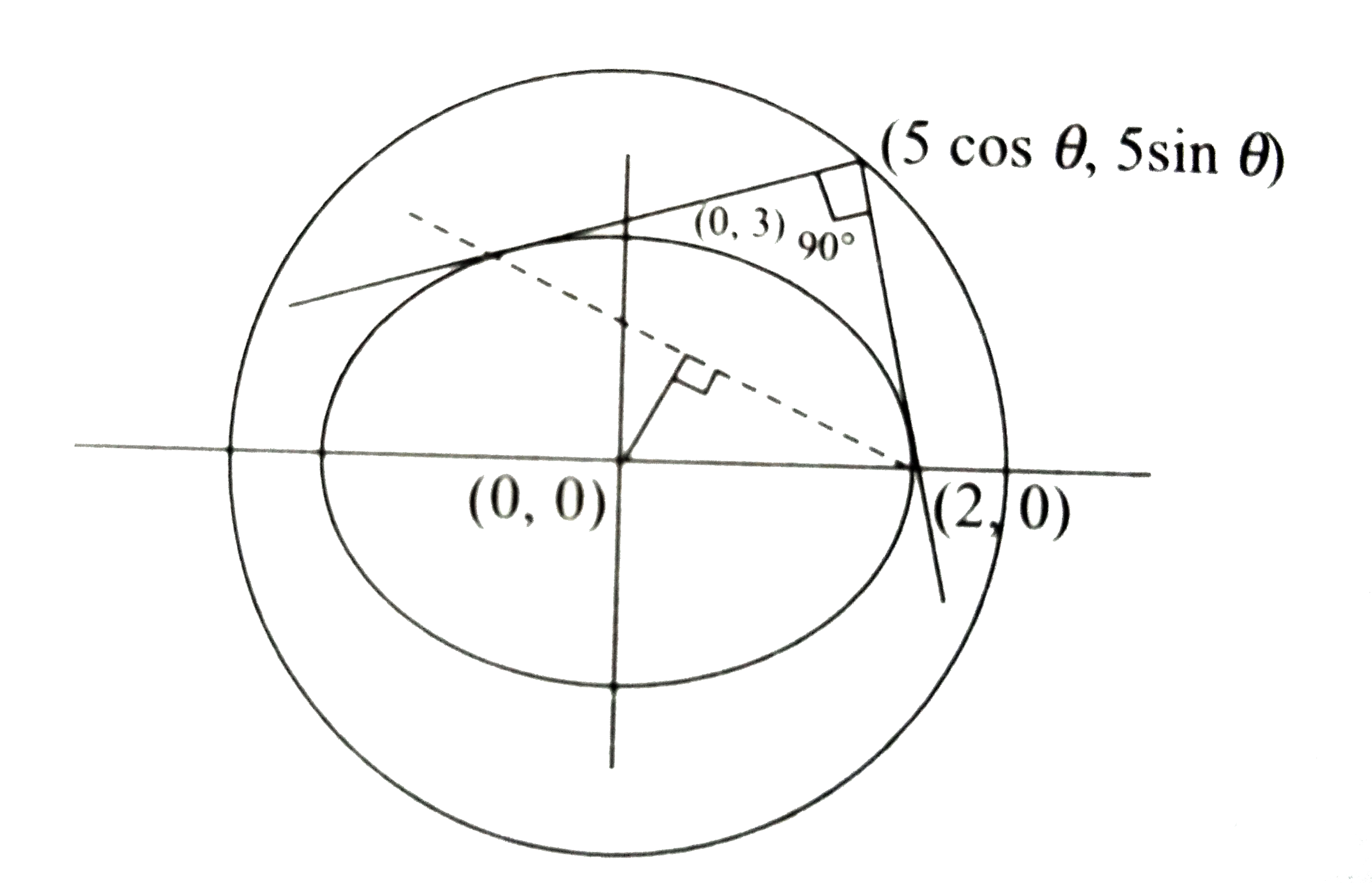
A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- For the ellipse (x^(2))/(16)+(y^(2))/(9)=1 .If The maximum distance f...
Text Solution
|
- If the distance of the centre of the ellipse 4(x-2y+1)^(2)+9(2x+y+2)^(...
Text Solution
|
- If the tangents from the point (lambda, 3) to the ellipse x^2/9+y^2/4=...
Text Solution
|
- The maximum distance of the centre of the ellipse (x^(2))/(16) +(y^(2)...
Text Solution
|
- Two perpendicular tangents to the ellipse (x^2)/(16)+(y^2)/(9)=1 are s...
Text Solution
|
- For the ellipse (x^(2))/(16)+(y^(2))/(9)=1 .If The maximum distance f...
Text Solution
|
- The locus of the foot of the perpendicular drawn from the centre on an...
Text Solution
|
- Prove that the chords of contact of pairs of perpendicular tangents to...
Text Solution
|
- Prove that the chords of contact of pairs of perpendicular tangents to...
Text Solution
|