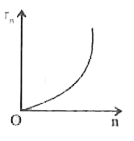
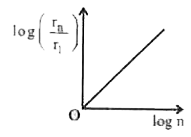
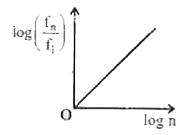
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
DISHA PUBLICATION-ATOMS-EXERCISE-2: CONCEPT APPLICATOR
- A 12.5eV electron beam is used to bombard gaseous hydrogen at room tem...
Text Solution
|
- Orbits of a particle moving in a circle are such that the perimeter of...
Text Solution
|
- A stationary hydrogen atom emits photon corresponding to the first lin...
Text Solution
|
- Which of the plots shown in the figure represents speed (vn) of the el...
Text Solution
|
- The diagram shows the energy levels for an electron in a certain atom....
Text Solution
|
- In the Bohr model an electron moves in a circular orbit around the pro...
Text Solution
|
- An electron , in a hydrogen-like atom, is in excited state. It has a t...
Text Solution
|
- The ionization energy of a hydrogen like Bohr atom is 4 Rydbergs. If, ...
Text Solution
|
- The wavelength of K(alpha) X-rays of two metals A and B are 4 // 1875 ...
Text Solution
|
- Suppose an electron is attracted toward the origin by a force(k)/(r ) ...
Text Solution
|
- In the Bohr model of a pi-mesic atom , a pi-mesic of mass m(pi) and of...
Text Solution
|
- If in hydrogen atom, radius of n^(th) Bohr orbit is rn., frequency of ...
Text Solution
|
- In the Bohr model of a hydrogen atom, the centripetal force is furnish...
Text Solution
|
- An electron in the hydrogen atom jumps from excited state n to the gro...
Text Solution
|
- In the Bohr's model of hydrogen-like atom the force between the nucleu...
Text Solution
|
- the wavelength of radiation emitted is lambda0 when an electron jumps....
Text Solution
|
- In Bohr's model of the hydrogen atom, let R, V, T and E represent the ...
Text Solution
|
- An electron in hydrogen atom makes a transition ni to n2 where n1 and...
Text Solution
|
- The ionization enegry of the electron in the hydrogen atom in its grou...
Text Solution
|
- If potential energy between a proton and an electron is given by | U |...
Text Solution
|