Similar Questions
Explore conceptually related problems
Recommended Questions
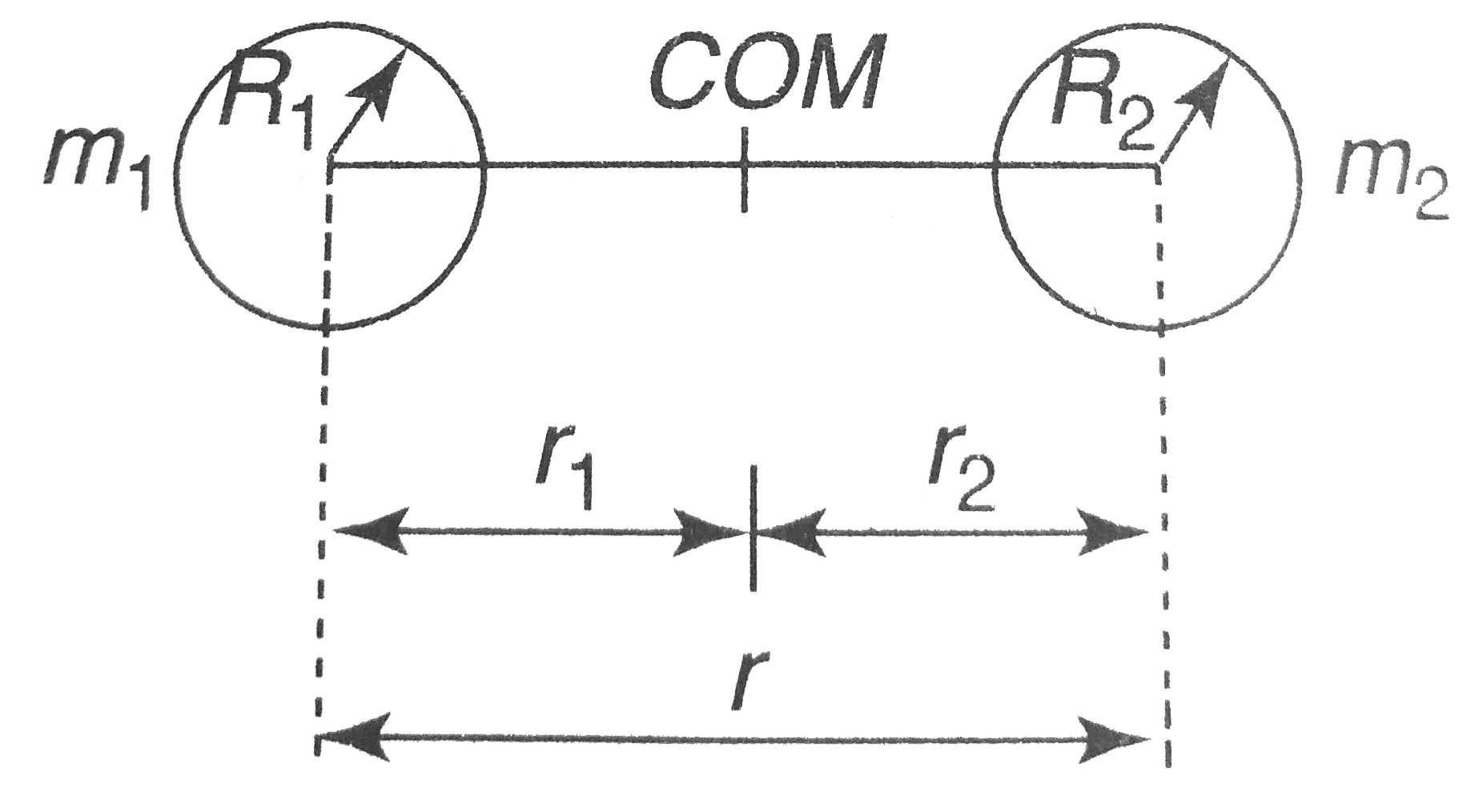
- Binary stars of comparable masses rotates under the influence of each ...
Text Solution
|
- A binary star consists of two stars A(mass 2.2 Ms) and B (mass 11 Ms) ...
Text Solution
|
- Binary stars of comparable masses m(1) and m(2) rotate under the influ...
Text Solution
|
- Binary stars of comparable masses rotates under the influence of each ...
Text Solution
|
- In a binary star system one star has thrice the mass of other. The sta...
Text Solution
|
- Binary stars rotate under mutual gravitational force at separation 2(G...
Text Solution
|
- A binary star system is revolving in a circular path with angular spee...
Text Solution
|
- A binary star consists of two stars A ( mass 2.2 Ms) and B (mass 11 M...
Text Solution
|
- A binary star consists of two stars A (mass 2.2M(s) ), and B of mass (...
Text Solution
|