Text Solution
Verified by Experts
Topper's Solved these Questions
UNITS AND MEASUREMENT
RESNICK AND HALLIDAY|Exercise PROBLEM|20 VideosUNITS AND MEASUREMENT
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)|31 VideosTHE NUCLEUS
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS(Integer Type)|7 VideosVECTORS
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS|39 Videos
Similar Questions
Explore conceptually related problems
RESNICK AND HALLIDAY-UNITS AND MEASUREMENT -PRACTICE QUESTIONS (MATRIX-MATCH)
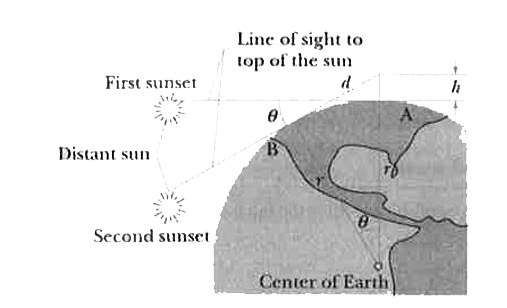
- When the sun appears to be just on horizon, it is in fact below the ho...
Text Solution
|
- Match Column I (Event) with Column II (order of the time interval for ...
Text Solution
|
- Match the physical quantities in Column I with the units given in Colu...
Text Solution
|
- The physical quantities, their formulae and dimensions expressed in te...
Text Solution
|
- The physical quantities, their formulae and dimensions expressed in te...
Text Solution
|
- The physical quantities, their formulae and dimensions expressed in te...
Text Solution
|
- Suppose two students trying to make a new measurement system so that t...
Text Solution
|
- Suppose two students trying to make a new measurement system so that t...
Text Solution
|
- Suppose two students are trying to make a new measurement system so th...
Text Solution
|
- If voltage V=(100pm5) V and current I=(10pm0.2) A, the percentage err...
Text Solution
|
- A dence collection of equal number of electrona and positive ions is ...
Text Solution
|
- The time period of oscillation of a simple pendulum is given by T=2pis...
Text Solution
|