Text Solution
Verified by Experts
Topper's Solved these Questions
OSCILLATIONS
RESNICK AND HALLIDAY|Exercise Checkpoint|8 VideosOSCILLATIONS
RESNICK AND HALLIDAY|Exercise Problems|39 VideosMOTION IN TWO AND THREE DIMENSIONS
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS (MATRIX-MATCH)|10 VideosPHOTONS AND MATTER WAVES
RESNICK AND HALLIDAY|Exercise PRACTICE QUESTIONS(Integer Type)|4 Videos
RESNICK AND HALLIDAY-OSCILLATIONS-Practice Questions
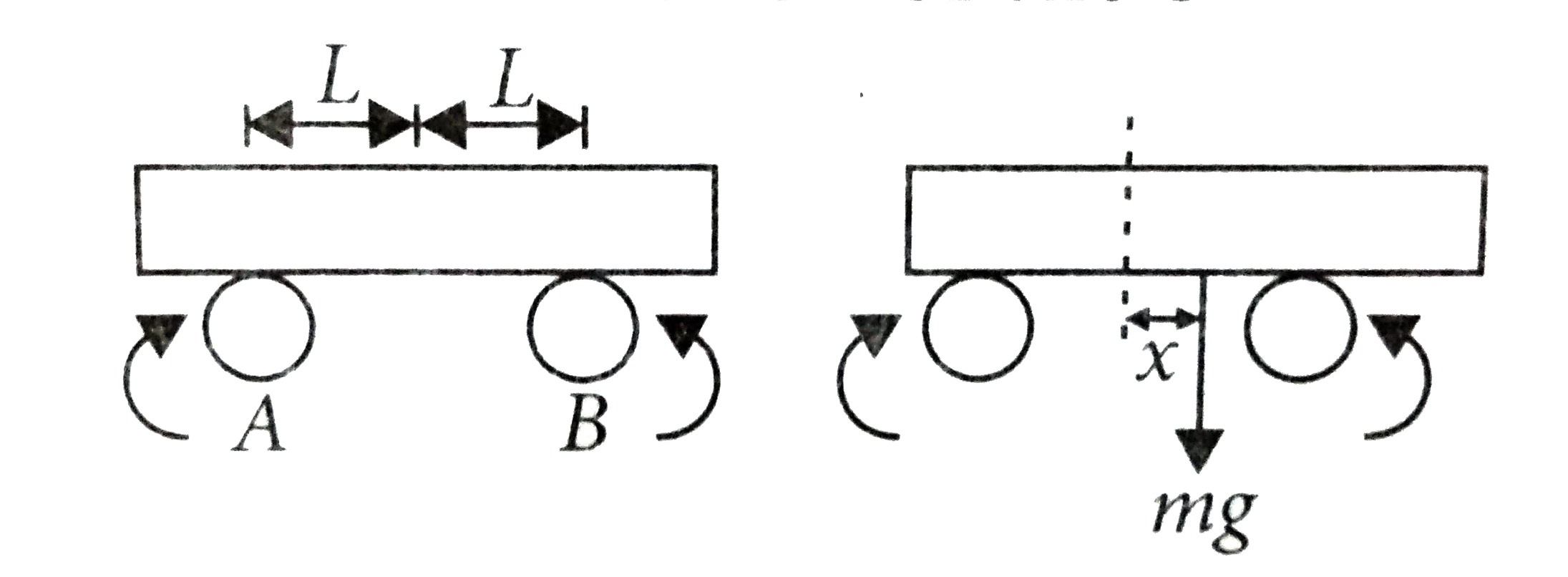
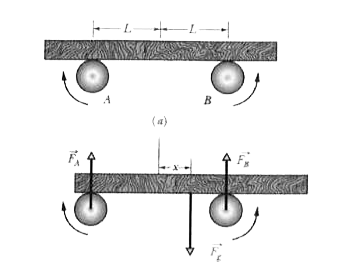
- A uniform bar with mass m lies symmetrically across two rapidly rotati...
Text Solution
|
- Which one of the following statement is true concerning an object exec...
Text Solution
|
- Resonance occurs in harmonic motion when
Text Solution
|
- A simple pendulum has length L and period T. As it passes through its ...
Text Solution
|
- An object of mass m, oscillating on the end of a spring with spring co...
Text Solution
|
- The velocity of a certain simple harmonic oscillator is given by v= -(...
Text Solution
|
- A 0.20kg object mass attached to a spring whose spring constant is 500...
Text Solution
|
- A ball hung from a vertical spring oscillates in simple harmonic motio...
Text Solution
|
- A 1.2kg mass is oscillating without friction on a spring whose spring ...
Text Solution
|
- The displacement of an object oscillating on a spring is given by x(t)...
Text Solution
|
- The displacement of an object oscillating on a spring is given by x(t)...
Text Solution
|
- A 0.25kg block oscillates on the end of the spring with a spring const...
Text Solution
|
- The amplitude of oscillation of a simple pendulum is increased from 1^...
Text Solution
|
- A particle undergoes damped harmonic motion. The spring constant is 10...
Text Solution
|
- Five particles undergo damped harmonic motion. Value for the spring co...
Text Solution
|
- A particle is osicllating according to the equation X= 7 cos (0.5 pi t...
Text Solution
|
- An archer pulls the bowstring back for a distance of 0.470m befor rele...
Text Solution
|
- A simple pendulum is made from a 0.65m long string and a small ball at...
Text Solution
|
- The length of a simple pendulum is 0.79m and the mass of the particle ...
Text Solution
|
- A block is attached to a horizontal spring and oscillates back and for...
Text Solution
|
- A copper rod (length =2.0m, radius =3.0 xx 10^(-3)m) hangs down from t...
Text Solution
|